题目内容
 如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.(Ⅰ)求证:FC∥平面EAD;
(Ⅱ)求直线FA与平面FBC所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出BC∥平面ADE,BF∥∥平面ADE,由此证明平面ADE∥平面BCF,从而得到FC∥平面EAD.
(Ⅱ)连接AC,设AC∩BD=O,连接FO,由OA,OB,OF两两垂直,建立空间直角坐标系O-xyz,利用向量法能求出直线FA与平面FBC所成角的正弦值.
(Ⅱ)连接AC,设AC∩BD=O,连接FO,由OA,OB,OF两两垂直,建立空间直角坐标系O-xyz,利用向量法能求出直线FA与平面FBC所成角的正弦值.
解答:
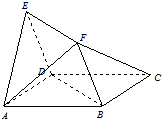 (Ⅰ)证明:∵四边形ABCD为菱形,∴BC∥AD,
(Ⅰ)证明:∵四边形ABCD为菱形,∴BC∥AD,
∵AD?平面ADE,BC不包含于平面ADE,
∴BC∥平面ADE,…(2分)
同理BF∥∥平面ADE,…(3分)
∵BC∩BF=B,
∴平面ADE∥平面BCF,…(4分)
∵FC?平面BCF,∴FC∥平面EAD.…(5分)
(Ⅱ)连接AC,
∵四边形ABCD是菱形,∴AC⊥BD.
设AC∩BD=O,连接FO,
∵FA=FC,O为AC中点,∴FO⊥AC,
∵四边形BDEF是菱形,且∠DBF=60°,
∴△DBF为等边三角形
∵O为BD中点,∴FO⊥BD,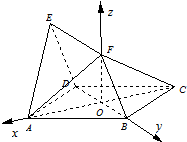
∴FO⊥平面ABCD,…(6分)
∴OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O-xyz,…(7分)
设AB=2,∵四边形ABCD是菱形,∠DAB=60°,∴BD=2,
∴OB=1,OA=OF=
,
∴O(0,0,0),A(
,0,0),B(0,1,0),C(-
,0,0),
F(0,0,
),D(0,-1,0),
∴
=(
,1,0),
=(0,-1,
),
设
=(x,y,z)为平面FBC的法向量,
则有
,
取y=-
,得
=(1,-
,-1).…(9分)
又∵
=(
,0-
),设直线FA与平面FBC所成的角为θ,
∴sinθ=|cos<
,
>|=
=
.
∴直线FA与平面FBC所成角的正弦值为
.…(13分)
 (Ⅰ)证明:∵四边形ABCD为菱形,∴BC∥AD,
(Ⅰ)证明:∵四边形ABCD为菱形,∴BC∥AD,∵AD?平面ADE,BC不包含于平面ADE,
∴BC∥平面ADE,…(2分)
同理BF∥∥平面ADE,…(3分)
∵BC∩BF=B,
∴平面ADE∥平面BCF,…(4分)
∵FC?平面BCF,∴FC∥平面EAD.…(5分)
(Ⅱ)连接AC,
∵四边形ABCD是菱形,∴AC⊥BD.
设AC∩BD=O,连接FO,
∵FA=FC,O为AC中点,∴FO⊥AC,
∵四边形BDEF是菱形,且∠DBF=60°,
∴△DBF为等边三角形
∵O为BD中点,∴FO⊥BD,

∴FO⊥平面ABCD,…(6分)
∴OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O-xyz,…(7分)
设AB=2,∵四边形ABCD是菱形,∠DAB=60°,∴BD=2,
∴OB=1,OA=OF=
| 3 |
∴O(0,0,0),A(
| 3 |
| 3 |
F(0,0,
| 3 |
∴
| CB |
| 3 |
| BF |
| 3 |
设
| n |
则有
|
取y=-
| 3 |
| n |
| 3 |
又∵
| FA |
| 3 |
| 3 |
∴sinθ=|cos<
| FA |
| n |
| ||||
|
| ||
| 5 |
∴直线FA与平面FBC所成角的正弦值为
| ||
| 5 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
设U=R,若集合M={x|-1<x≤2},则∁UM=( )
| A、(-∞,-1] |
| B、(2,+∞) |
| C、(-∞,-1]∪[2,+∞) |
| D、(-∞,-1]∪(2,+∞) |
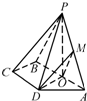 如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=
如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=