题目内容
在等比数列{an}中,其前n项和为Sn,已知a3=
,S3=
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在正整数n,使得Sn-Sn+2=
?,并说明理由.
| 3 |
| 2 |
| 9 |
| 2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在正整数n,使得Sn-Sn+2=
| 3 |
| 32 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设等比数列{an}的公比为q,由已知条件可解得q和首项,可得通项公式;
(Ⅱ)分类讨论,当q=1时不合题意,当a1=6,q=-
时可得n的方程,解得n值,综合可得.
(Ⅱ)分类讨论,当q=1时不合题意,当a1=6,q=-
| 1 |
| 2 |
解答:
解:(Ⅰ)设等比数列{an}的公比为q,
则S3=a1+a2+a3=a3(q-2+q-1+1)=
,
由a3=
可得q-2+q-1+1=3,
整理可得2q2-q-1=0,解得q=1,或q=-
,
当q=1时,an=a3=
,
当q=-
时,可得a1=6,an=6×(-
)n-1;
(Ⅱ)由(Ⅰ)知,当q=1时,Sn=
n,Sn-Sn-2=3≠
,
当a1=6,q=-
时,Sn=
=4[1-(-
)n],
由Sn-Sn-2=
可得4[1-(-
)n]-4[1-(-
)n-2]=
,
化简可得-3(-
)n=
,即(-
)n=-
,解得n=5
综上可得存在正整数n=5,使得Sn-Sn+2=
则S3=a1+a2+a3=a3(q-2+q-1+1)=
| 9 |
| 2 |
由a3=
| 3 |
| 2 |
整理可得2q2-q-1=0,解得q=1,或q=-
| 1 |
| 2 |
当q=1时,an=a3=
| 3 |
| 2 |
当q=-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)知,当q=1时,Sn=
| 3 |
| 2 |
| 3 |
| 32 |
当a1=6,q=-
| 1 |
| 2 |
6[1-(-
| ||
1-(-
|
| 1 |
| 2 |
由Sn-Sn-2=
| 3 |
| 32 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 32 |
化简可得-3(-
| 1 |
| 2 |
| 3 |
| 32 |
| 1 |
| 2 |
| 1 |
| 32 |
综上可得存在正整数n=5,使得Sn-Sn+2=
| 3 |
| 32 |
点评:本题考查等比数列的性质,涉及分类讨论的思想,属中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
设不等式x2-x≤0的解集为M,函数f(x)=lg(1-|x|)的定义域为N,则M∩N=( )
| A、(-1,0] |
| B、[0,1) |
| C、(0,1) |
| D、[0,1] |
等差数列{an}中,an>0,a12+a72+2a1a7=4,则它的前7项的和等于( )
A、
| ||
| B、5 | ||
C、
| ||
| D、7 |
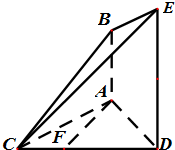 已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F在线段CD上.
已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F在线段CD上. 如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC. 已知向量
已知向量