题目内容
13.已知抛物线C:y2=4x的焦点为F,点P(2,t)为抛物线C上一点,则|PF|等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 利用抛物线的性质,转化求解|PF|即可.
解答 解:抛物线C:y2=4x的焦点为F(1,0),点P(2,t)为抛物线C上一点,由抛物线的定义可知,
则|PF|等于P到准线方程的距离,即:2+1=3.
故选:B.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
4.若i为虚数单位,a,b∈R,且$\frac{a+2i}{I}$=b+i,则复数a+bi的模等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
2.已知全集U={x|y=log2(x-1)},集合A={x||x-2|<1},则∁UA=( )
| A. | (3,+∞) | B. | [3,+∞) | C. | (1,3) | D. | (-∞,1] |
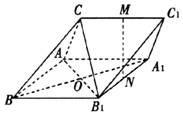 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.