题目内容

3．已知椭圆$\frac{x^2}{25}+\frac{y^2}{b^2}=1（b＞0）$（0＜b＜5）的离心率$\frac{4}{5}$，则b的值等于（　　）
A．1B．3C．6D．8

分析 根据题意，由椭圆的标准方程分析可得其焦点在x轴上，计算可得c的值，由椭圆的离心率公式可得e=$\frac{c}{a}$=$\frac{\sqrt{25-{b}^{2}}}{5}$=$\frac{4}{5}$，解可得b的值，即可得答案．

解答 解：根据题意，椭圆的方程为$\frac{x^2}{25}+\frac{y^2}{b^2}=1（b＞0）$，
又由0＜b＜5，则椭圆的焦点在x轴上，
则c=$\sqrt{25-{b}^{2}}$，
又由其离心率e=$\frac{c}{a}$=$\frac{\sqrt{25-{b}^{2}}}{5}$=$\frac{4}{5}$，
解可得b=3；
故选：B．

点评 本题考查椭圆的标准方程，注意先分析椭圆的焦点的位置．

练习册系列答案
相关题目
13．如图，已知长方形ABCD中，AB=2$\sqrt{2}$，AD=$\sqrt{2}$，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．
（1）求证：AD⊥BM；
（2）求直线DB与平面ABCM所成角的正弦值．
14．已知函数$f（x）=\frac{1}{x}$，则f'（2）等于（　　）
A．4B．$\frac{1}{4}$C．-4D．$-\frac{1}{4}$
11．（Ⅰ）已知函数f（x）=|2x-3|-2|x|，若关于x不等式f（x）≤|a+2|+2a恒成立，求实数a的取值范围；
（Ⅱ）已知正数x，y，z，满足2x+y+z=1，求$\frac{1}{x+2y+z}$+$\frac{3}{z+3x}$的最小值．
18．已知直线l1：2x-3y+1=0，直线l2过点（1，1）且与直线l1垂直．
（1）求直线l2的方程；
（2）求直线l2与两坐标轴围成的三角形的面积．
8．（1）已知α∈（$\frac{π}{2}$，π），且sin$\frac{α}{2}$+cos$\frac{α}{2}$=$\frac{\sqrt{6}}{2}$，求cosα的值；
（2）已知sin（θ+$\frac{π}{4}$）=$\frac{3}{5}$，求cos（$\frac{π}{4}$-θ）．
15．数列{an}的前n项和记为Sn，a1=l，an+1=2Sn+1 （n≥1）
（I）求{ an }的通项公式；
（Ⅱ）等差数列{bn}的各项为正，其前n项和为Tn，且T3=15，又a1+b1，a2+b2，a3+b3成等比数列，求数列{$\frac{1}{{T}_{n}}$}的前n项和An．
12．运行如图所示的程序框图，则输出结果为（　　）
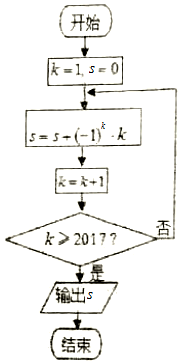
A．2017B．2016C．1009D．1008
13．已知抛物线C：y2=4x的焦点为F，点P（2，t）为抛物线C上一点，则|PF|等于（　　）
A．2B．3C．4D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网