题目内容
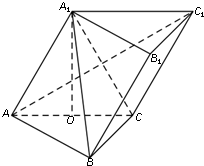 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)若AA1=2,求三棱锥C-A1AB的高的大小.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明AC1⊥平面A1BC,只需证明AC1⊥BC、AC1⊥A1C;
(Ⅱ)利用VC-A1AB=VA-A1BC,求三棱锥C-A1AB的高的大小.
(Ⅱ)利用VC-A1AB=VA-A1BC,求三棱锥C-A1AB的高的大小.
解答:
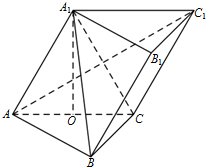 (Ⅰ)证明:因为A1O⊥平面ABC,所以A1O⊥BC.
(Ⅰ)证明:因为A1O⊥平面ABC,所以A1O⊥BC.
又BC⊥AC,所以BC⊥平面A1ACC1,所以AC1⊥BC.…(2分)
因为AA1=AC,所以四边形A1ACC1是菱形,所以AC1⊥A1C.
所以AC1⊥平面A1BC.…(6分)
(Ⅱ)解:设三棱锥C-A1AB的高为h.
由(Ⅰ)可知,三棱锥A-A1BC的高为
AC1=
.
因为VC-A1AB=VA-A1BC,即
S△A1ABh=
S△A1BC•
.
在△A1AB中,AB=A1B=2
,AA1=2,所以S△A1AB=
.…(10分)
在△A1BC中,BC=A1C=2,∠BCA1=90°,所以S△A1BC=
BC•A1C=2.
所以h=
.…(12分)
 (Ⅰ)证明:因为A1O⊥平面ABC,所以A1O⊥BC.
(Ⅰ)证明:因为A1O⊥平面ABC,所以A1O⊥BC.又BC⊥AC,所以BC⊥平面A1ACC1,所以AC1⊥BC.…(2分)
因为AA1=AC,所以四边形A1ACC1是菱形,所以AC1⊥A1C.
所以AC1⊥平面A1BC.…(6分)
(Ⅱ)解:设三棱锥C-A1AB的高为h.
由(Ⅰ)可知,三棱锥A-A1BC的高为
| 1 |
| 2 |
| 3 |
因为VC-A1AB=VA-A1BC,即
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
在△A1AB中,AB=A1B=2
| 2 |
| 7 |
在△A1BC中,BC=A1C=2,∠BCA1=90°,所以S△A1BC=
| 1 |
| 2 |
所以h=
2
| ||
| 7 |
点评:本题考查直线与平面垂直的证明,考查点到平面距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
集合A={x|2x-3≤0},B={x|-1≤x<2},则A∪B=( )
A、{x|-
| ||
| B、{x|x<2} | ||
C、{x|-1≤x<
| ||
D、{x|x≤
|
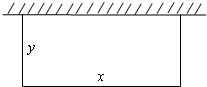 一段长为20米的篱笆围成一个一边靠墙的矩形菜园,墙长18米.如图,设菜园与墙平行的边长为x米,另一边长为y米.
一段长为20米的篱笆围成一个一边靠墙的矩形菜园,墙长18米.如图,设菜园与墙平行的边长为x米,另一边长为y米. 如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.
如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.