题目内容
已知x是第三象限角，且cosx-sinx
．
（1）求cosx+sinx的值；
（2）求2sin2x-sinxcosx+cos2x的值．
| ||
| 5 |
（1）求cosx+sinx的值；
（2）求2sin2x-sinxcosx+cos2x的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）对已知等式等号两边平方求得2sinxcosx的值，进而根据配方法求得（cosx+sinx）2，进而x的范围确定cosx+sinx的值，最后求得cosx+sinx的值．
解答：
解：（1）（cosx-sinx）2=1-2sinxcosx=
，
∴2sinxcosx=
，
∴（cosx+sinx）2=1+2sinxcosx=
，
∵x是第三象限，
∴cosx+sinx＜0，
∴cosx+sinx=-
．
（2）由（1）得
，求得cosx=-
，sinx=-
，
∴2sin2x-sinxcosx+cos2x=2×
-
×
+
=
．
| 1 |
| 5 |
∴2sinxcosx=
| 4 |
| 5 |
∴（cosx+sinx）2=1+2sinxcosx=
| 9 |
| 5 |
∵x是第三象限，
∴cosx+sinx＜0，
∴cosx+sinx=-
3
| ||
| 5 |
（2）由（1）得
|
| ||
| 5 |
2
| ||
| 5 |
∴2sin2x-sinxcosx+cos2x=2×
| 4 |
| 5 |
| ||
| 5 |
2
| ||
| 5 |
| 1 |
| 5 |
| 7 |
| 5 |
点评：本题主要考查了同角三角函数基本关系的应用．解题过程中特别注意三角函数的符号．
练习册系列答案
全能测控一本好卷系列答案
相关题目
阅读程序框图（如图），执行相应的程序，输出的结果是（ ）
| A、50 | B、55 |
| C、1023 | D、2565 |
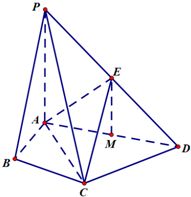在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，M为AD的中点，PA=2AB=4．
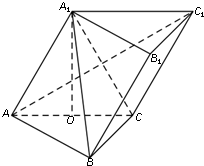如图，在斜三棱柱ABC-A1B1C1中，O是AC的中点，A1O⊥平面ABC，∠BCA=90°，AA1=AC=BC．
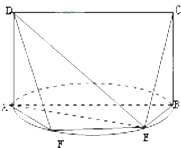如图，E是以AB为直径的半圆上异于点A、B的点，矩形ABCD所在的平面垂直于该半圆所在平面，且AB=2AD=2．