题目内容
集合A={x|2x-3≤0},B={x|-1≤x<2},则A∪B=( )
A、{x|-
| ||
| B、{x|x<2} | ||
C、{x|-1≤x<
| ||
D、{x|x≤
|
考点:并集及其运算
专题:集合
分析:利用不等式的性质和并集定义求解.
解答:
解:∵集合A={x|2x-3≤0}={x|x≤
},B={x|-1≤x<2},
∴A∪B={x|x<2}.
故选:B.
| 3 |
| 2 |
∴A∪B={x|x<2}.
故选:B.
点评:本题考查并集的计算,是基础题,解题时要注意不等式性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果正整数a的各位数字之和等于8,那么称a为“幸运数”(如:8,35,440,2015等均为“幸运数”),将所有“幸运数”从小到大排成一列a1,a2,a3,…,则2015是( )
| A、第83个 | B、第84个 |
| C、第85个 | D、第86个 |
已知数列的通项公式an=2n-37,则Sn取最小值时n=( )
| A、18 | B、19 |
| C、18或19 | D、20 |
复数z满足z(2+i)=2i-1,则复数z的实部与虚部之和为( )
| A、1 | B、-1 | C、2 | D、3 |
阅读程序框图(如图),执行相应的程序,输出的结果是( )


| A、50 | B、55 |
| C、1023 | D、2565 |
已知实数x,y满足ax<ay(a>1),则下列关系式恒成立的是( )
A、
| ||||
| B、ln(x2+1)<ln(y2+1) | ||||
| C、sinx<siny | ||||
| D、x3<y3 |
在数列{an}中,a1=1,an+2+(-1)nan=2,记Sn为数列{an}的前项和,则S61=( )
| A、931 | B、961 |
| C、991 | D、1021 |
圆心在直线l:x-y+1=0上,且过A(1,1),B(2,-2)两点的圆的方程为( )
| A、(x-3)2+(y-2)2=25 |
| B、(x+3)2+(y-2)2=25 |
| C、(x-3)2+(y+2)2=25 |
| D、(x+3)2+(y+2)2=25 |
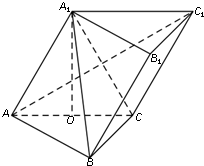 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.