题目内容
 如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.
如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.(Ⅰ)若P是BC的中点,证明AP∥平面BFG;
(Ⅱ)求四面体ABEG的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取BF中点Q,连PQ、GQ,则PQ∥CF,且PQ=
CF=AG=1,证明AP∥平面BFG,只需证明AP∥GQ;
(Ⅱ)证明DE⊥平面ABCD,即可求四面体ABEG的体积.
| 1 |
| 2 |
(Ⅱ)证明DE⊥平面ABCD,即可求四面体ABEG的体积.
解答:
(Ⅰ)证明:取BF中点Q,连PQ、GQ,则PQ∥CF,且PQ=
CF=AG=1,
∵CDEF是正方形,DE⊥平面ABCD,
∴CF⊥平面ABCD,
∴PQ⊥平面ABCD,
又AG⊥平面ABCD,
∴PQ∥AG,APQG为矩形,
∴AP∥GQ
∵QG?平面BFG,AP?平面BFG,
∴AP∥平面BFG…6分
(Ⅱ)解:∵AG⊥平面ABCD,∴AG⊥AD,
又ABCD是矩形,∴AB⊥AD
从而AD⊥平面ABG
又DE⊥平面ABCD,∴AG∥DE
∴VABEG=VE-ABG=VD-ABG=
×
×AB×AG×AD=
…12分.
| 1 |
| 2 |
∵CDEF是正方形,DE⊥平面ABCD,
∴CF⊥平面ABCD,
∴PQ⊥平面ABCD,
又AG⊥平面ABCD,
∴PQ∥AG,APQG为矩形,
∴AP∥GQ
∵QG?平面BFG,AP?平面BFG,
∴AP∥平面BFG…6分
(Ⅱ)解:∵AG⊥平面ABCD,∴AG⊥AD,
又ABCD是矩形,∴AB⊥AD
从而AD⊥平面ABG
又DE⊥平面ABCD,∴AG∥DE
∴VABEG=VE-ABG=VD-ABG=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题综合考查空间线、面的位置关系,体积的计算,中等题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知实数x,y满足ax<ay(a>1),则下列关系式恒成立的是( )
A、
| ||||
| B、ln(x2+1)<ln(y2+1) | ||||
| C、sinx<siny | ||||
| D、x3<y3 |
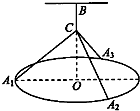 如图,一个圆环O直径为4m,通过铁丝CA1,CA2,CA3,BC(A1,A2,A3是圆上三等分点)悬挂在B处,圆环呈水平状态,并距天花板2m,记四段铁丝总长为y(m).
如图,一个圆环O直径为4m,通过铁丝CA1,CA2,CA3,BC(A1,A2,A3是圆上三等分点)悬挂在B处,圆环呈水平状态,并距天花板2m,记四段铁丝总长为y(m).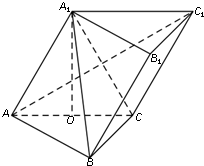 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.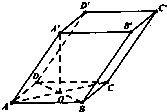 如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=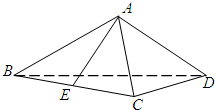 如图,在体积为
如图,在体积为