题目内容
设函数f（x）=2x+a，g（x）=
（x2+3），若g（f（x））=x2+x+1，求f（x）的解析式．
| 1 |
| 4 |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由题意可得g（f（x））的解析式，和已知作比较可得a的不等式组，解之可得a值，可得f（x）解析式．
解答：
解：∵f（x）=2x+a，g（x）=
（x2+3），
∴g（f（x））=
（2x+a）2+
=x2+ax+
a2+
，
又∵g（f（x））=x2+x+1，
∴x2+x+1=x2+ax+
a2+
，
∴
，解得a=1，
∴f（x）的解析式为：f（x）=2x+1
| 1 |
| 4 |
∴g（f（x））=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
又∵g（f（x））=x2+x+1，
∴x2+x+1=x2+ax+
| 1 |
| 4 |
| 3 |
| 4 |
∴
|
∴f（x）的解析式为：f（x）=2x+1
点评：本题考查函数解析式的求解，待定系数是解决问题的关键，属基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
下列语句中是简单命题是（ ）
A、
| ||
| B、△ABC是等腰直角三角形 | ||
| C、负数的平方是正数 | ||
| D、3x+2＜0 |
在下列四个命题中
①y=1是幂函数；
②“x＜1”是“x＜2”的充分不必要条件；
③命题“存在x∈R，x2-2＞0”的否定是：“任意x∈R，x2-x＜0”
④若a=-1，则函数f（x）=ax2+2x-1只有一个零点．
其中错误的个数有（ ）个．
①y=1是幂函数；
②“x＜1”是“x＜2”的充分不必要条件；
③命题“存在x∈R，x2-2＞0”的否定是：“任意x∈R，x2-x＜0”
④若a=-1，则函数f（x）=ax2+2x-1只有一个零点．
其中错误的个数有（ ）个．
| A、4 | B、2 | C、3 | D、1 |
已知集合A={x||2x+1|＞3}，集合B={x|y=
}，则A∩（∁RB）=（ ）
|
| A、（1，2） |
| B、（1，2] |
| C、（1，+∞） |
| D、[1，2] |
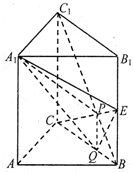如图在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AA1=2，E是BB1的中点，且CE交BC1于点P，点Q在线段BC上，CQ=2QB．
某商家推出一款简单电子游戏，弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上（如图），用S表示这三个球为顶点的三角形的面积．规定：当三球共线时，S=0；当S最大时，中一等奖，当S最小时，中二等奖，其余情况不中奖，一次游戏只能弹射一次．