题目内容
6.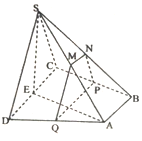 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|(1)当λ=$\frac{1}{2}$时,求证:平面SAE⊥平面MNPQ
(2)是否存在实数λ,使得三棱锥Q-BCN的体积为$\frac{7}{16}$?若存在,求出实数λ的值,若不存在,说明理由.
分析 (1)由直角梯形性质可得PQ⊥AE,结合PQ⊥SE得出PQ⊥平面SAE,故而平面SAE⊥平面MNPQ;
(2)根据VQ-BCN=VN-BCQ=$\frac{1}{3}$S△BCQ•$\frac{1}{2}SE$列方程解出λ.
解答 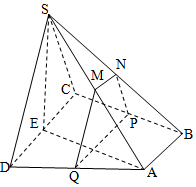 解:(1)E为CD中点,所以四边形ABCE为矩形,所以AE⊥CD
解:(1)E为CD中点,所以四边形ABCE为矩形,所以AE⊥CD
当λ=$\frac{1}{2}$时,Q为AD中点,PQ∥CD 所以PQ⊥AE
因为平面SCD⊥平面ABCD,SE⊥CD,所以SE⊥面ABCD
因为PQ?面ABCD,所以PQ⊥SE 所以PQ⊥面SAE
所以面MNPQ⊥面SAE…(6分)
(2)VQ-BCN=VN-BCQ=$\frac{1}{2}$VS-BCQ=$\frac{1}{2}$×$\frac{1}{3}$×S△BCQ•h,
∵SC=SD,E为CD中点∴SE⊥CD
又∵平面SCD⊥平面ABCD,平面SCD∩平面ABCD=CD,SE?平面SCD,
∴SE⊥平面ABCD∴SE即为S到平面BCQ的距离,即SE=h.
在△SCD中,SC=SD=CD=2,∴SE=$\sqrt{3}$,
在直角梯形ABCD中,易求得:BC=$\sqrt{3}$,
∵M,N为中点,∴MN∥AB,∴AB∥平面MNPQ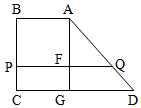 ,
,
又∵平面MNPQ∩平面ABCD=PQ,∴AB∥PQ,
又∵AB⊥BC,∴PQ⊥BC,∴S△BCQ=$\frac{1}{2}$BC×PQ=$\frac{\sqrt{3}}{2}$PQ,
∴VQ-BCN=$\frac{1}{2}$×$\frac{1}{3}$×S△BCQ•h=$\frac{1}{2}$×$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$PQ×$\sqrt{3}$=$\frac{1}{4}$PQ,
由题意:$\frac{1}{4}$PQ=$\frac{7}{16}$,∴PQ=$\frac{7}{4}$.
在梯形ABCD中,$\frac{FQ}{GD}$=$\frac{AQ}{AD}$,FQ=PQ-AB=$\frac{3}{4}$,GD=1,∴$\frac{AQ}{AD}$=$\frac{3}{4}$.
∴$\frac{DQ}{AD}$=$\frac{1}{4}$ 即λ=$\frac{1}{4}$
∴存在实数λ=$\frac{1}{4}$,使得三棱锥Q-BCN的体积为$\frac{7}{16}$.
点评 本题考查了面面垂直的判定与性质,线面垂直的判定与性质,棱锥的体积计算,属于中档题.

| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | $\frac{16π}{3}$ | B. | $\frac{40π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{80π}{3}$ |
| A. | 98 | B. | 49 | C. | 14 | D. | 147 |
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
| A. | (-1,1) | B. | (-1,1] | C. | [1,2) | D. | [1,2] |
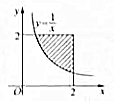 在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.
在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.