题目内容
11.在△ABC中,AC=$\sqrt{13}$,BC=1,B=60°,则△ABC的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
分析 由已知利用余弦定理可求AB的值,进而利用三角形面积公式即可计算得解.
解答 解:∵AC=$\sqrt{13}$,BC=1,B=60°,
∴由余弦定理可得:AC2=AB2+BC2-2AB•BC•sinB,即:13=AB2+1-AB,
∴解得:AB=4或-3(舍去),
∴S△ABC=$\frac{1}{2}$AB•BC•sinB=$\frac{1}{2}×4×1×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
故选:A.
点评 本题主要考查了余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
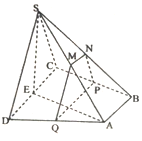 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
