题目内容
13.已知α∈($\frac{π}{2}$,π),且sin$\frac{α}{2}$+cos $\frac{α}{2}$=$\frac{\sqrt{6}}{2}$.(1)求tan(α+$\frac{π}{4}$)的值;
(2)若sin(α-β)=-$\frac{3}{5}$,β∈($\frac{π}{2}$,π),求cos β的值.
分析 (1)利用两边平方,可得sinα的值,利用同角三角函数关系式求解cosα,可得tanα.可求tan(α+$\frac{π}{4}$)的值;
(2)根据cosβ=cos[α-(α-β)]根据两角和与差的公式打开,可求cos β的值.
解答 解(1)∵sin$\frac{α}{2}$+cos $\frac{α}{2}$=$\frac{\sqrt{6}}{2}$.
∴1+sinα=$\frac{3}{2}$,即sinα=$\frac{1}{2}$
∵α∈($\frac{π}{2}$,π),
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{\sqrt{3}}{2}$.
∴tanα=$\frac{sinα}{cosα}=-\frac{\sqrt{3}}{3}$.
那么:tan(α+$\frac{π}{4}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanα•tan\frac{π}{4}}=\frac{15-7\sqrt{3}}{13}$;
(2)∵sin α=$\frac{1}{2}$.又$\frac{π}{2}$<α<π,
∴cos α=-$\sqrt{1-sin2α}$=-$\frac{\sqrt{3}}{2}$.
∵$\frac{π}{2}$<α<π,$\frac{π}{2}$<β<π,
∴-$\frac{π}{2}$<α-β<$\frac{π}{2}$.
又sin(α-β)=-$\frac{3}{5}$,得cos(α-β)=$\frac{4}{5}$.
cos β=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=-$\frac{\sqrt{3}}{2}$×$\frac{4}{5}$+$\frac{1}{2}$×$\frac{3}{5}$=$-\frac{4\sqrt{3}-3}{10}$.
点评 本题主要考查了同角三角函数关系式和构造思想,构造cosβ=cos[α-(α-β)]利用两角和与差的公式打开求解是关键.属于基础题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案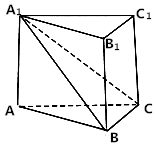 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.(1)求证:AB⊥BC;
(2)若∠CAB=$\frac{π}{6}$,求三棱锥B1-A1BC的体积.
| x | 18 | 13 | 10 | -1 |
| y | 24 | 34 | 38 | 64 |
| A. | 65度 | B. | 68度 | C. | 70度 | D. | 72度 |
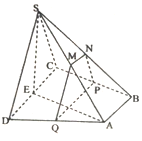 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|