题目内容
若不等式mx2+mnx+n>0的解集为{x|1<x<2},则m+n的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由题意,得出不等式对应的方程的两个实数根x1,x2;再由根与系数的关系,求出m、n的值即可.
解答:
解:∵不等式mx2+mnx+n>0的解集为{x|1<x<2},
∴m<0,且方程mx2+mnx+n=0的解为x1=1,x2=2;
∴由根与系数的关系,得
;
解得
,
∴m+n=-
-3=-
.
故选:D.
∴m<0,且方程mx2+mnx+n=0的解为x1=1,x2=2;
∴由根与系数的关系,得
|
解得
|
∴m+n=-
| 3 |
| 2 |
| 9 |
| 2 |
故选:D.
点评:本题考查了一元二次不等式的解法应用问题,解题时根据一元二次不等式与对应方程的关系来解答,是基础题.

练习册系列答案
相关题目
若函数f(x)=
f′(-1)x2-2x+3,则f′(-1)的值为( )
| 1 |
| 2 |
| A、0 | B、-1 | C、1 | D、2 |
C的方程为(x-1)2+(y-2)2=4,则圆C的圆心坐标和半径r分别为( )
| A、(1,2),r=2 |
| B、(-1,-2),r=2 |
| C、(1,2),r=4 |
| D、(-1,-2),r=4 |
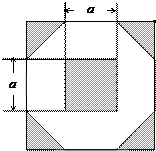 为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )| A、2a2 |
| B、3a2 |
| C、4a2 |
| D、5a2 |
圆C1:x2+y2=1与圆C2:(x-2)2+y2=1的位置关系是( )
| A、相离 | B、相交 | C、内切 | D、外切 |
(x2-1)(
-2)5的展开式的常数项是( )
| 1 |
| x |
| A、48 | B、-48 |
| C、112 | D、-112 |
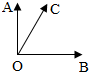 如图所示:|
如图所示:|| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 6 |
| OC |
| OA |
| OB |
| λ |
| μ |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
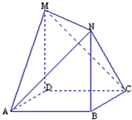 四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.
四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.