题目内容
已知函数f(x)=2cos2
+sinx.
(1)求f(x)的最小正周期和单调递增区间;
(2)求f(x)在区间[0,π]上的最大值与最小值.
| x |
| 2 |
(1)求f(x)的最小正周期和单调递增区间;
(2)求f(x)在区间[0,π]上的最大值与最小值.
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)利用倍角公式和两角和差的正弦公式、正弦函数的性质即可得出;
(2)利用正弦函数的单调性即可得出.
(2)利用正弦函数的单调性即可得出.
解答:
解:(1)函数f(x)=2cos2
+sinx=cosx+1+sinx=
sin(x+
)+1.
∴函数f(x)的最小正周期是2π,
由2kπ-
≤x+
≤2kπ+
,解得2kπ-
≤x≤2kπ+
(k∈Z).
∴函数f(x)的单调递增区间为[2kπ-
,2kπ+
](k∈Z).)
(2)由(1)函数f(x)=
sin(x+
)+1.
∵x∈[0,π],
≤x+
≤
,
当x+
=
时,即x=
时,sin(x+
)=1,此时f(x)取得最大值
+1;
当x+
=
,即x=π时,sin(x+
)=-
,此f(x)取得最小值0.
| x |
| 2 |
| 2 |
| π |
| 4 |
∴函数f(x)的最小正周期是2π,
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
∴函数f(x)的单调递增区间为[2kπ-
| 3π |
| 4 |
| π |
| 4 |
(2)由(1)函数f(x)=
| 2 |
| π |
| 4 |
∵x∈[0,π],
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
当x+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
当x+
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| ||
| 2 |
点评:本题考查了倍角公式、两角和差的正弦公式、正弦函数的性质,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
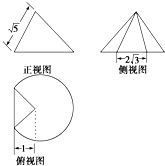 一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
△ABC中,∠C=120°,a,b是方程x2-3x+2=0的两根,则c的值为( )
| A、3 | ||
| B、7 | ||
C、
| ||
D、
|
设△ABC的内角A、B、C的对边分别为a、b、c,若
=
=
,则△ABC是( )
| a | ||
cos
|
| b | ||
cos
|
| c | ||
cos
|
| A、直角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 把一个正方形等分成九个相等的小正方形,将中间的一个正方形挖掉如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖掉,得图(2);如此继续下去…,第三个图中共挖掉
把一个正方形等分成九个相等的小正方形,将中间的一个正方形挖掉如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖掉,得图(2);如此继续下去…,第三个图中共挖掉