题目内容
双曲线渐近线方程为y=±
x,且实轴长为2,则此双曲线的标准方程为 .
| 1 |
| 2 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线的简单性质求解.
解答:
解:∵双曲线渐近线方程为y=±
x,且实轴长为2,
∴当焦点在x轴时,
,解得a=1,b=
,
双曲线标准方程为x2-4y2=1.
当焦点在y轴时,
,解得a=1,b=2,
双曲线标准方程为y2-
=1.
故答案为:x2-4y21或y2-
=1.
| 1 |
| 2 |
∴当焦点在x轴时,
|
| 1 |
| 2 |
双曲线标准方程为x2-4y2=1.
当焦点在y轴时,
|
双曲线标准方程为y2-
| x2 |
| 4 |
故答案为:x2-4y21或y2-
| x2 |
| 4 |
点评:本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
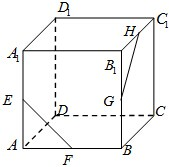 如图,在正方体ABCDA1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCDA1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于( )| A、30° | B、45° |
| C、60° | D、90° |
函数y=tan2x的最小正周期是( )
| A、π | ||
B、
| ||
C、
| ||
| D、2π |
若a=21.2,b=(
)-0.8,c=2log52,则( )
| 1 |
| 2 |
| A、c<b<a |
| B、b<a<c |
| C、c<a<b |
| D、b<c<a |