Question

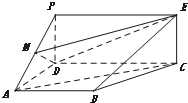如图，PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD=

1

2

CD=1，PD=

2

．
（Ⅰ）若M为PA中点，求证：AC∥平面MDE；
（Ⅱ）求直线PA与平面PBC所成角的正弦值．

Answer 1

考点：直线与平面所成的角,直线与平面平行的判定

专题：空间位置关系与距离

分析：（I）连结PC交DE于N，易证AC∥MN．由线面平行的判定定理可得；（II）由垂直关系可以D为原点，以DA，DC，DP所在的直线分别为x，y，z轴建立空间直角坐标系，
设平面PBC的法向量为

n

=（x，y，z），可求得

n

=（1，1，

2

），设直线PA与平面PBC所成角为θ，则sinθ=|cos＜

AP

，

n

＞|，代值计算可得．

解答： 解：（I）在矩形PDCE中，连结PC交DE于N，则点N为PC的中点．
在△APC中，点M为PA的中点，点N为PC的中点，
∴AC∥MN．又MN?平面MDE，AC?平面MDE，∴AC∥平面MDE
（II）由∠ADC=90°可得AD⊥CD．
由平面PDCE⊥平面ABCD，且平面PDCE∩平面ABCD=CD，
可得AD⊥平面PDCE，∴AD⊥PD，又矩形PDCE中PD⊥CD，
以D为原点，以DA，DC，DP所在的直线分别为x，y，z轴建立空间直角坐标系，
则A（1，0，0），P（0，0，

2

），B（1，1，0），C（0，2，0），
∴

AP

=（-1，0，

2

），

CP

=（0，-2，

2

），

BC

=（-1，1，0）
设平面PBC的法向量为

n

=（x，y，z），
则

CP

•

n

=-2y+

2

z=0，且

BC

•

n

=-x+y=0，
取y=1可得x=1，z=

2

，

n

=（1，1，

2

），
设直线PA与平面PBC所成角为θ，则sinθ=|cos＜

AP

，

n

＞|=

| AP • n |

| AP || n |

=

3

6

点评：本题考查直线与平面平行的判定和直线与平面所成的角，建立空间直角坐标系是解决问题的关键，属中档题．