题目内容
函数y=f(x)为定义在R上的减函数,函数y=f(x-1)的图象关于点(1,0)对称,x,y满足不等式f(x2-2x)+f(2y-y2)≤0,M(1,2),N(x,y),O为坐标原点,当1≤x≤4时,求出
•
的取值范围.
| OM |
| ON |
考点:基本不等式,平面向量数量积的运算
专题:不等式的解法及应用
分析:设P(x,y)为函数y=f(x-1)的图象上的任意一点,关于(1,0)对称点为(2-x,-y),可得f(2-x-1)=-f(x-1),即f(1-x)=-f(x-1).由于不等式f(x2-2x)+f(2y-y2)≤0化为f(x2-2x)≤-f(2y-y2)=f(y2-2y),再利用函数y=f(x)为定义在R上的减函数,可得x2-2x≥y2-2y,即即
或
又∵1≤x≤4,画出可行域.M(1,2),N(x,y),O为坐标原点,∴
•
=x+2y=t.进而得出答案.
|
|
| OM |
| ON |
解答:
解:设P(x,y)为函数y=f(x-1)的图象上的任意一点,关于(1,0)对称点为(2-x,-y),
∴f(2-x-1)=-f(x-1),即f(1-x)=-f(x-1).
∴不等式f(x2-2x)+f(2y-y2)≤0化为f(x2-2x)≤-f(2y-y2)=f(1-1-2y+y2)=f(y2-2y),
∵函数y=f(x)为定义在R上的减函数,
∴x2-2x≥y2-2y,
化为(x-1)2≥(y-1)2,
∵函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,即y=f(x)为奇函数,
又函数y=f(x)在R上的为减函数,
化为(x-1)2≥(y-1)2,
即
或
又∵1≤x≤4,画出可行域.
M(1,2),N(x,y),O为坐标原点,∴
•
=x+2y=t.
化为y=-
x+
.
由图可知:当直线y=-
x+
经过点A(4,-2)时,t取得最小值0.
当直线y=-
x+
经过点B(4,4)时t取得最大值4+2×4=12.
综上可得:
•
的取值范围是[0,12].

∴f(2-x-1)=-f(x-1),即f(1-x)=-f(x-1).
∴不等式f(x2-2x)+f(2y-y2)≤0化为f(x2-2x)≤-f(2y-y2)=f(1-1-2y+y2)=f(y2-2y),
∵函数y=f(x)为定义在R上的减函数,
∴x2-2x≥y2-2y,
化为(x-1)2≥(y-1)2,
∵函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,即y=f(x)为奇函数,
又函数y=f(x)在R上的为减函数,
化为(x-1)2≥(y-1)2,
即
|
|
又∵1≤x≤4,画出可行域.
M(1,2),N(x,y),O为坐标原点,∴
| OM |
| ON |
化为y=-
| 1 |
| 2 |
| t |
| 2 |
由图可知:当直线y=-
| 1 |
| 2 |
| t |
| 2 |
当直线y=-
| 1 |
| 2 |
| t |
| 2 |
综上可得:
| OM |
| ON |
点评:本题综合考查了函数的对称性、单调性、线性规划的可行域及其最值、直线的平移等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
函数f(x)=min{
,|x-2|},其中min{a,b}=
,若动直线y=m与函数y=f(x)的图象有三个不同的交点,则实数m的取值范围是( )
| x |
|
| A、(0,1) |
| B、(1,3) |
| C、[0,1] |
| D、[1,3] |
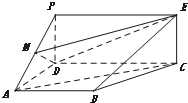 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= 如图,在△ABC中,|
如图,在△ABC中,|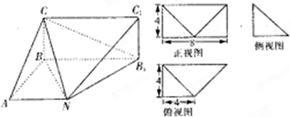 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角表,俯视图为直角梯形.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角表,俯视图为直角梯形.