题目内容
函数y=xcosx-sinx，x∈（0，2π）单调增区间是 ．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求导，进而利用导数与函数的单调性的关系即可得出．
解答：
解：∵函数y=xcosx-sinx，x∈（0，2π），
∴y′=-xsinx，
由-xsinx＞0，x∈（0，2π），
化为sinx＜0，x∈（0，2π），
解得π＜x＜2π．
故函数y=xcosx-sinx，x∈（0，2π）单调增区间是（π，2π）．
故答案为（π，2π）．
∴y′=-xsinx，
由-xsinx＞0，x∈（0，2π），
化为sinx＜0，x∈（0，2π），
解得π＜x＜2π．
故函数y=xcosx-sinx，x∈（0，2π）单调增区间是（π，2π）．
故答案为（π，2π）．
点评：熟练掌握利用导数研究函数的单调性的方法是解题的关键．
练习册系列答案
相关题目
已知a=log30.3，b=20.2，c=0.30.3，则a，b，c三者的大小关系是（ ）
| A、c＞b＞a |
| B、b＞a＞c |
| C、a＞b＞c |
| D、b＞c＞a |
与函数y=x有相同图象的一个函数是（ ）
A、y=
| ||
| B、y=logaax（a＞0，a≠1） | ||
C、y=（
| ||
D、y=
|
如图，在长方体A1B1C1D1-ABCD中，AD=CD=4，AD1=5，M是线段B1D1的中点．（1）求证：BM∥平面D1AC；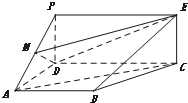
如图，PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD=