题目内容
已知函数f(x)=x3-(k2-k+1)x2+5x-2,g(x)=k2x2+kx+1,其中k∈R,若函数F(x)=f(x)+g(x)在区间(0,3)上不单调,则k的取值范围为( )
| A、[-4,-2) |
| B、(-3,-1] |
| C、(-5,-2] |
| D、(-5,-2) |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:因F(x)=f(x)+g(x)=x3+(k-1)x2+(k+5)x-1,先求导数:F′(x),因F(x)在区间(0,3)上不单调,得到F′(x)=0在(0,3)上有实数解,且无重根,再利用分离参数的方法得出k,最后再利用导数求出此函数的值域即可;
解答:
解:因F(x)=f(x)+g(x)=x3+(k-1)x2+(k+5)x-1,
F′(x)=3x2+2(k-1)x+(k+5),
因F(x)在区间(0,3)上不单调,
所以F′(x)=0在(0,3)上有实数解,且无重根,
由F′(x)=0得k(2x+1)=-(3x2-2x+5),
∴k=-
=-
[(2x+1)+
-
],
令t=2x+1,有t∈(1,7),记h(t)=t+
,
则h(t)在(1,3]上单调递减,在[3,7)上单调递增,
所以有h(t)∈[6,10),于是(2x+1)+
∈[6,10)
得k∈(-5,-2],而当k=-2时有F′(x)=0在(0,3)上有两个相等的实根x=1,故舍去,
所以k∈(-5,-2);
故选:D.
F′(x)=3x2+2(k-1)x+(k+5),
因F(x)在区间(0,3)上不单调,
所以F′(x)=0在(0,3)上有实数解,且无重根,
由F′(x)=0得k(2x+1)=-(3x2-2x+5),
∴k=-
| 3x2-2x+5 |
| 2x+1 |
| 3 |
| 4 |
| 9 |
| 2x+1 |
| 10 |
| 3 |
令t=2x+1,有t∈(1,7),记h(t)=t+
| 9 |
| t |
则h(t)在(1,3]上单调递减,在[3,7)上单调递增,
所以有h(t)∈[6,10),于是(2x+1)+
| 9 |
| 2x+1 |
得k∈(-5,-2],而当k=-2时有F′(x)=0在(0,3)上有两个相等的实根x=1,故舍去,
所以k∈(-5,-2);
故选:D.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,同时考查了分析与解决问题的综合能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知一圆锥的侧面展开图是一个中心角为直角的扇形,若该圆锥的侧面积为4π,则该圆锥的体积为( )
A、
| ||||
B、
| ||||
| C、3π | ||||
D、
|
已知a=log30.3,b=20.2,c=0.30.3,则a,b,c三者的大小关系是( )
| A、c>b>a |
| B、b>a>c |
| C、a>b>c |
| D、b>c>a |
过三棱锥高的中点与底面平行的平面把这个三棱锥分为两部分,则这上、下两部分体积之比为( )
| A、1:7 | B、1:4 |
| C、2:3 | D、1:8 |
一个平行于棱锥底面的截面与棱锥的底面的面积之比为1:9,则截面把棱锥的高分成两段的长度之比为
( )
( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=min{
,|x-2|},其中min{a,b}=
,若动直线y=m与函数y=f(x)的图象有三个不同的交点,则实数m的取值范围是( )
| x |
|
| A、(0,1) |
| B、(1,3) |
| C、[0,1] |
| D、[1,3] |
与函数y=x有相同图象的一个函数是( )
A、y=
| ||
| B、y=logaax(a>0,a≠1) | ||
C、y=(
| ||
D、y=
|
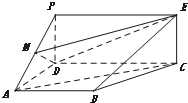 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=