题目内容
正项数列{an}满足an2-(2n-1)an-2n=0
(1)求数列{an}的通项公式an
(2)令bn=2n-1•an,求数列{bn}的前项和Tn.
(1)求数列{an}的通项公式an
(2)令bn=2n-1•an,求数列{bn}的前项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件得(an-2n)(an+1)=0,由an>0,得an=2n.
(2)由bn=2n-1•an=n•2n,利用错位相减求和法能求出数列{bn}的前项和Tn.
(2)由bn=2n-1•an=n•2n,利用错位相减求和法能求出数列{bn}的前项和Tn.
解答:
解:(1)∵正项数列{an}满足an2-(2n-1)an-2n=0,
∴(an-2n)(an+1)=0,
∵an>0,∴an=2n.
(2)bn=2n-1•an=n•2n,
∴Tn=1•2+2•22+3•23+…+n•2n,①
2Tn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得:-Tn=2+22+23+…+2n-n•2n+1
=
-n•2n+1
=2n+1-2-n•2n+1,
∴Tn=(n-1)•2n+1+2.
∴(an-2n)(an+1)=0,
∵an>0,∴an=2n.
(2)bn=2n-1•an=n•2n,
∴Tn=1•2+2•22+3•23+…+n•2n,①
2Tn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得:-Tn=2+22+23+…+2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
=2n+1-2-n•2n+1,
∴Tn=(n-1)•2n+1+2.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
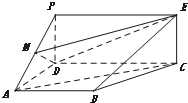 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= 在长方体ABCD-A1B1C1D1中,AD=AB=
在长方体ABCD-A1B1C1D1中,AD=AB=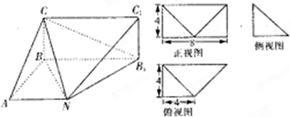 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角表,俯视图为直角梯形.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角表,俯视图为直角梯形.