题目内容
若正实数a，b满足ab=a+b+3，则a+b的取值范围是 ．
考点：基本不等式
专题：不等式的解法及应用
分析：正实数a，b满足ab=a+b+3，利用基本不等式可得：3+a+b=ab≤(
)2，再利用一元二次不等式的解法即可得出．
| a+b |
| 2 |
解答：
解：∵正实数a，b满足ab=a+b+3，
∴3+a+b=ab≤(
)2，当且仅当a=b时取等号．
令a+b=t＞0，则t2-4t-12≥0，
解得t≥6．
即a+b的取值范围是[6，+∞）．
故答案为：[6，+∞）．
∴3+a+b=ab≤(
| a+b |
| 2 |
令a+b=t＞0，则t2-4t-12≥0，
解得t≥6．
即a+b的取值范围是[6，+∞）．
故答案为：[6，+∞）．
点评：本题考查了基本不等式的性质、一元二次不等式的解法，考查了计算能力，属于基础题．
练习册系列答案
相关题目
过三棱锥高的中点与底面平行的平面把这个三棱锥分为两部分，则这上、下两部分体积之比为（ ）
| A、1：7 | B、1：4 |
| C、2：3 | D、1：8 |
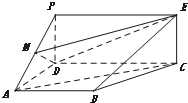如图，PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD=
在长方体ABCD-A1B1C1D1中，AD=AB=