题目内容
若平面向量
=（3，5），
=（-2，1），则
-2
的坐标为（ ）
| a |
| b |
| a |
| b |
| A、（7，3） |
| B、（7，7） |
| C、（1，7） |
| D、（1，3） |
考点：平面向量的坐标运算
专题：平面向量及应用
分析：根据平面向量的坐标运算，进行计算即可．
解答：
解：∵平面向量
=（3，5），
=（-2，1），
∴
-2
=（3-2×（-2），5-2×1）=（7，3）．
故选：A．
| a |
| b |
∴
| a |
| b |
故选：A．
点评：本题考查了平面向量的坐标运算问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
=（-1，-2），
=（m2，4），那么“
∥
”是“m=
”（ ）
| a |
| b |
| a |
| b |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知命题p：?x∈[0，+∞），x≥sinx，命题q：?x∈R，sinx+cosx≥2，则（ ）
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧（￢q）是真命题 |
| D、命题p∧（￢q）是假命题 |
若a=0.95.1，b=5.10.9，c=log0.95.1，则a、b、c三者的大小关系是（ ）
| A、a＜b＜c |
| B、b＜c＜a |
| C、c＜b＜a |
| D、c＜a＜b |
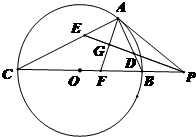如图：已知PA与圆O相切于点A，经过点O的割线PBC交圆O于点B，C，∠APC的平分线分别交AB，AC于点D，E，．点G是线段ED的中点，AG的延长线与CP相交于点F．双曲线
-
=1（a＞0，b＞0）的离心率为2，则它的一条渐近线经过点（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） | ||
| B、（2，1） | ||
C、（1，
| ||
D、（
|