题目内容
4.无穷等比数列{an}的前n项和为Sn,若S3=6,S6=3,则$\underset{lim}{n→∞}{S}_{n}$=$\frac{8+4\root{3}{4}}{2+\root{3}{4}}$.分析 利用等比数列前n项和公式求出首项及公比,由此能求出等比数列的前n项和的极限.
解答 解:∵无穷等比数列{an}的前n项和为Sn,若S3=6,S6=3,
∴$\left\{\begin{array}{l}{{S}_{3}=\frac{{a}_{1}(1-{q}^{3})}{1-q}=6}\\{{S}_{6}=\frac{{a}_{1}(1-{q}^{6})}{1-q}=3}\end{array}\right.$,解得${a}_{1}=4+2\root{3}{4}$,q=-$\frac{\root{3}{4}}{2}$,
∴Sn=$\frac{(4+2\root{3}{4})[1-(-\frac{\root{3}{4}}{2})^{n}]}{1+\frac{\root{3}{4}}{2}}$,
∴$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}$$\frac{(4+2\root{3}{4})[1-(-\frac{\root{3}{4}}{2})^{n}]}{1+\frac{\root{3}{4}}{2}}$=$\frac{4+2\root{3}{4}}{1+\frac{\root{3}{4}}{2}}$=$\frac{8+4\root{3}{4}}{2+\root{3}{4}}$.
故答案为:$\frac{8+4\root{3}{4}}{2+\root{3}{4}}$.
点评 本题考查等比数列的前n项和的极值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设等比数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=3,则$\frac{{a}_{11}}{{a}_{2}}$( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
19.已知数列{an}满足an+1=$\left\{\begin{array}{l}2{a_n}({0≤{a_n}<\frac{1}{2}})\\ 2{a_n}-1({\frac{1}{2}≤{a_n}<1})\end{array}$若a1=$\frac{6}{7}$,则a2012的值为( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
9.“$\frac{1}{a}$>$\frac{1}{b}$”是“a<b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.平面α上有不共线三点到平面β的距离相等,则α与β的位置关系为( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 垂直 |
13.以下命题中错误的是( )
| A. | 若直线与平面没有公共点,则它们平行 | |
| B. | 如果两直线没有公共点,那么这两直线平行 | |
| C. | 若两平面没有公共点,则它们平行 | |
| D. | 若一个平面经过另一个平面的一条垂线,则这两个平面垂直 |
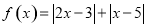 .
.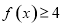 的解集;
的解集;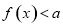 的解集不是空集,求实数
的解集不是空集,求实数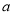 的取值范围.
的取值范围. 在点
在点 处的切线的斜率为
处的切线的斜率为 ,则函数
,则函数 的部分图象可以为( )
的部分图象可以为( )