题目内容
19.已知数列{an}满足an+1=$\left\{\begin{array}{l}2{a_n}({0≤{a_n}<\frac{1}{2}})\\ 2{a_n}-1({\frac{1}{2}≤{a_n}<1})\end{array}$若a1=$\frac{6}{7}$,则a2012的值为( )| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
分析 由已知数列递推式结合首项求出数列前几项,可得数列{an}是以3为周期的周期数列,由此求得a2012的值.
解答 解:由已知数列递推式an+1=$\left\{\begin{array}{l}2{a_n}({0≤{a_n}<\frac{1}{2}})\\ 2{a_n}-1({\frac{1}{2}≤{a_n}<1})\end{array}$,且a1=$\frac{6}{7}$,
求得${a}_{2}=\frac{5}{7}$,${a}_{3}=\frac{3}{7}$,${a}_{4}=\frac{6}{7}$,…
由上可知,数列{an}是以3为周期的周期数列,
则a2012=${a}_{3×670+2}={a}_{2}=\frac{5}{7}$.
故选:C.
点评 本题考查数列递推式,关键在于对数列周期的发现,是基础题.

练习册系列答案
相关题目
11.已知x,y满足$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+1≥0}\\{x+2y-2≥0}\end{array}\right.$,若z=3x-2y的最大值为a,最小值为b,则ab=( )
| A. | -12 | B. | -9 | C. | 3 | D. | 6 |
8.在各项均为正数的等比数列{an}中,a2a10=9,则a5+a7( )
| A. | 有最小值6 | B. | 有最大值6 | C. | 有最大值9 | D. | 有最小值3 |
 满足
满足 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
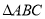 中,角
中,角 ,
,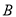 ,
,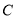 的对边分别是
的对边分别是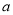 ,
,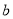 ,
,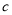 ,
, 为
为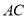 边上的高,
边上的高,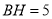 ,若
,若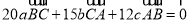 ,则
,则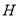 到
到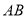 边的距离为( )
边的距离为( )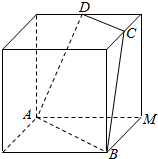 如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.
如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.