题目内容
14.已知函数f(x)对任意的x,y∈R,总有f(x+y)=f(x)+f(y)+1,(1)设函数g(x)=f(x)+1,判断函数g(x)的奇偶性并证明;
(2)若x<0时恒有f(x)>-1,判断函数f(x)的单调性并证明.
分析 (1)根据条件能得出g(x+y)=g(x)+g(y),再用奇偶性的定义加以证明;
(2)直接运用单调性的定义和作差比较法证明函数的单调性.
解答 解:(1)∵f(x+y)=f(x)+f(y)+1,
∴f(x+y)+1=[f(x)+1]+[f(y)+1],(*)
而g(x)=f(x)+1,则(*)式可以表示为:
g(x+y)=g(x)+g(y),可以判断y=g(x)为R上的奇函数,证明如下:
令x=y=0得,g(0)=g(0)+g(0),所以,g(0)=0,
再令y=-x得,g(0)=g(x)+g(-x),所以,g(-x)=-g(x),
因此,g(x)为奇函数;
(2)f(x)为R上单调递减函数,证明如下:
任取x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)
=f(x1-x2)+f(x2)+1-f(x2)
=f(x1-x2)+1,
∵x1-x2<0,∴f(x1-x2)>-1,
故f(x1)-f(x2)>0,即f(x1)>f(x2)
所以f(x)为R上的单调递减函数.
点评 本题主要考查了抽象函数奇偶性的判断和证明,抽象函数单调性的判断和证明,运用了定义和作差比较法,属于中档题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
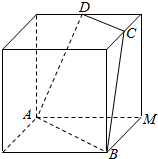 如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.
如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.