题目内容
(1)已知cos(
+x)=
,求
的值.
(2)已知cos(α-
)=-
,sin(
-β)=
,且
<α<π,0<β<
,求cos(α+β)的值.
| π |
| 4 |
| 3 |
| 5 |
| sin2x-2sin2x |
| 1-tanx |
(2)已知cos(α-
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
考点:两角和与差的余弦函数,三角函数的化简求值,两角和与差的正弦函数
专题:三角函数的求值
分析:(1)化简条件求得 cosx-sinx=
,平方可得sin2x=
.再化简要求的式子为sin2x,从而求得结果.
(2)根据
=(α-
)-(
-β),先求得sin(α-
)、cos(
-β)、cos
的值,再根据cos(α+β)=2cos2
-1,计算求得结果.
3
| ||
| 5 |
| 7 |
| 25 |
(2)根据
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| α+β |
| 2 |
| α+β |
| 2 |
解答:
解:(1)∵cos(
+x)=
,∴
(cosx-sinx)=
,∴cosx-sinx=
,
∴1-2sinx•cosx=
,∴sin2x=
.
又∵
=
=sin2x=
.
(2)∵
=(α-
)-(
-β),
∴cos
=cos[(α-
)-(
-β)]=cos(α-
)cos(
-β)+sin(α-
)sin(
-β).
又∵
<α<π,0<β<
,且cos(α-
)=-
,sin(
-β)=
,∴
<α-
<π,0<
-β<
,
∴sin(α-
)=
=
=
,cos(
-β)=
=
=
,
∴cos
=-
×
+
×
=
,
∴cos(α+β)=2cos2
-1=2×(
)2-1=-
.
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
3
| ||
| 5 |
∴1-2sinx•cosx=
| 18 |
| 25 |
| 7 |
| 25 |
又∵
| sin2x-2sin2x |
| 1-tanx |
| 2sinx•cosx(cosx-sinx) |
| cosx-sinx |
| 7 |
| 25 |
(2)∵
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
∴cos
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
又∵
| π |
| 2 |
| π |
| 2 |
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
| β |
| 2 |
| α |
| 2 |
| π |
| 2 |
∴sin(α-
| β |
| 2 |
1-cos2(α-
|
1-(-
|
4
| ||
| 9 |
| α |
| 2 |
1-sin2(
|
1-(
|
| ||
| 3 |
∴cos
| α+β |
| 2 |
| 1 |
| 9 |
| ||
| 3 |
4
| ||
| 9 |
| 2 |
| 3 |
7
| ||
| 27 |
∴cos(α+β)=2cos2
| α+β |
| 2 |
7
| ||
| 27 |
| 239 |
| 729 |
点评:本题主要考查三角函数的恒等变换及化简求值,要特别注意角的范围,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知函数f(x)=|x2-4|-3x+m恰有两个不同的零点,则实数m的取值范围是( )
A、(-6,6)∪(
| ||
B、(
| ||
C、(-∞,-
| ||
D、(-
|
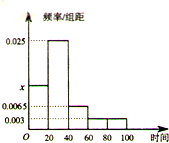 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100). 如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.
如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.