题目内容
设f(x)=-
x3+
ax2+2a2x(a∈R).
(Ⅰ)若f(x)在(
,+∞)上存在单调递增区间,求实数a的取值范围;
(Ⅱ)设函数g(x)=f(x)+
(1-a)x2+2a(1-a)x,若0<a<2,g(x)在[1,4]上的最小值为-
,求g(x)在该区间上的最大值.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)若f(x)在(
| 2 |
| 3 |
(Ⅱ)设函数g(x)=f(x)+
| 1 |
| 2 |
| 16 |
| 3 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知条件得f′(x)=-(x-2a)(x+a),由f′(x)≥0,得(x-2a)(x+a)≤0,由此结合已知条件能求出a的取值范围.
(Ⅱ)由已知条件得g(x)=-
x3+
x2+2ax,g′(x)=-(x-
)(x-
),由此结合已知条件能求出g(x)在区间[1,4]上的最大值.
(Ⅱ)由已知条件得g(x)=-
| 1 |
| 3 |
| 1 |
| 2 |
1+
| ||
| 2 |
1-
| ||
| 2 |
解答:
解:(Ⅰ)∵f(x)=-
x3+
ax2+2a2x(a∈R),
∴f′(x)=-x2+ax+2a2
=-(x-2a)(x+a),
由f′(x)≥0,得(x-2a)(x+a)≤0,
①当a=0时,有x2≤0,得x=0,不合题意;
②当a>0时,有-a<x<2a,
∵f(x)在(
,+∞)上存在递增区间,
∴2a>
,即a>
;
③当a<0时,有2a<x<-a,
∵f(x)在(
,+∞)上存在递增区间,
∴-a>
,即a<-
.
综上,a的取值范围为(-∞,-
)∪(
,+∞).
(Ⅱ)由已知g(x)=f(x)+
(1-a)x2+2a(1-a)x
=-
x3+
x2+2ax,
∴g′(x)=-x2+x+2a=-(x-
)(x-
),
∵0<a<2,∴
<0,
且t<
<
<4,
由g′(x)>0,得
<x<
,
∴g(x)在[1,
]上递增,在[
,4]上递减,
∴g(x)max=g(
),
又∵0<a<2,
∴g(4)-g(1)=(-
+8+8a)-(-
+
+2a)=6a-
<0,
∴g(4)<g(1),
∴在[1,4]上,函数g(x)min=g(4)=-
+8+8a=-
,
解得a=1,此时g(x)=-
x3+
x2+2x,
在[1,4]上,g(x)max=g(
)=g(2)=-
+2+4=
.
| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=-x2+ax+2a2
=-(x-2a)(x+a),
由f′(x)≥0,得(x-2a)(x+a)≤0,
①当a=0时,有x2≤0,得x=0,不合题意;
②当a>0时,有-a<x<2a,
∵f(x)在(
| 2 |
| 3 |
∴2a>
| 2 |
| 3 |
| 1 |
| 3 |
③当a<0时,有2a<x<-a,
∵f(x)在(
| 2 |
| 3 |
∴-a>
| 2 |
| 3 |
| 2 |
| 3 |
综上,a的取值范围为(-∞,-
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅱ)由已知g(x)=f(x)+
| 1 |
| 2 |
=-
| 1 |
| 3 |
| 1 |
| 2 |
∴g′(x)=-x2+x+2a=-(x-
1+
| ||
| 2 |
1-
| ||
| 2 |
∵0<a<2,∴
1-
| ||
| 2 |
且t<
1+
| ||
| 2 |
1+
| ||
| 2 |
由g′(x)>0,得
1-
| ||
| 2 |
1+
| ||
| 2 |
∴g(x)在[1,
1+
| ||
| 2 |
1+
| ||
| 2 |
∴g(x)max=g(
1+
| ||
| 2 |
又∵0<a<2,
∴g(4)-g(1)=(-
| 64 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 27 |
| 2 |
∴g(4)<g(1),
∴在[1,4]上,函数g(x)min=g(4)=-
| 64 |
| 3 |
| 16 |
| 3 |
解得a=1,此时g(x)=-
| 1 |
| 3 |
| 1 |
| 2 |
在[1,4]上,g(x)max=g(
1+
| ||
| 2 |
| 8 |
| 3 |
| 10 |
| 3 |
点评:本题考查满足条件的实数的取值范围的求法,考查函数在闭区间上的最大值的求法,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列1,3,6,10,x,21,…中,x的值是 ( )
| A、12 | B、13 | C、15 | D、16 |
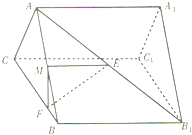 如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1的各棱长都相等,M、E分别是AB和AB1的中点,点F在BC上,且满足BF=1,FC=3.
如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1的各棱长都相等,M、E分别是AB和AB1的中点,点F在BC上,且满足BF=1,FC=3.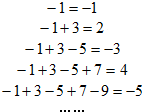 观察如图所示5个等式:照图中式子规律:
观察如图所示5个等式:照图中式子规律: