题目内容
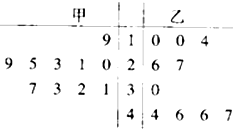 林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )
林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )| A、x甲>x乙,甲种树苗比乙种树苗高度更整齐 |
| B、x甲>x乙,乙种树苗比甲种树苗高度更整齐 |
| C、x甲<x乙,甲种树苗比乙种树苗高度更整齐 |
| D、x甲<x乙,乙种树苗比甲种树苗高度更整齐 |
考点:茎叶图
专题:概率与统计
分析:本题考查的知识点是茎叶图,由已知的茎叶图,可知甲、乙两种树苗抽取的样本高度,进而求出两组数据的平均数及方差,然后根据平均数的大小判断哪种树苗的平均高度高,根据方差判断哪种树苗长的整齐.
解答:
解:由茎叶图中的数据,我们可得甲、乙两种树苗抽取的样本高度分别为:
甲:19,20,21,23,25,29,31,32,33,37
乙:10,10,14,26,27,30,44,46,46,47
由已知易得:
=
(19+20+21+23+25+29+31+32+33+37)=27,
=
(10+10+14+26+27+30+44+46+46+47)=30,
S甲2<S乙2
故:乙种树苗的平均高度大于甲种树苗的平均高度,
甲种树苗比乙种树苗长得整齐.
故选C
甲:19,20,21,23,25,29,31,32,33,37
乙:10,10,14,26,27,30,44,46,46,47
由已知易得:
. |
| x甲 |
| 1 |
| 10 |
. |
| x乙 |
| 1 |
| 10 |
S甲2<S乙2
故:乙种树苗的平均高度大于甲种树苗的平均高度,
甲种树苗比乙种树苗长得整齐.
故选C
点评:本题考查了茎叶图;数据的离散程度与茎叶图形状的关系具体如下:茎叶图中各组数据的越往中间集中,表示数据离散度越小,其标准差越小;茎叶图中各组数据的越往两边离散,表示数据离散度越大,其标准差越大.

练习册系列答案
相关题目
数列{an},满足对任意的n∈N+,均有an+an+1+an+2为定值.若a7=2,a9=3,a98=4,则数列{an}的前100项的和S100=( )
| A、132 | B、299 |
| C、68 | D、99 |
集合A={α|α=
,k∈Z},B={β|β=
+
,n∈Z}的关系是( )
| kπ |
| 6 |
| nπ |
| 3 |
| π |
| 6 |
| A、A?B | B、A?B |
| C、A⊆B | D、A=B |
按照程序框图执行,第三个输出的数是( )


| A、7 | B、6 | C、5 | D、4 |
 一个社会调查机构就某地居民的月收入调查了10000人,并根所得数据画了样本的频率分布直方图(如图所示)为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在(2500,3000元/月)收入段应抽出( )人.
一个社会调查机构就某地居民的月收入调查了10000人,并根所得数据画了样本的频率分布直方图(如图所示)为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在(2500,3000元/月)收入段应抽出( )人.| A、10人 | B、15人 |
| C、20人 | D、25人 |
根据工作需要,现从4名女教师,a名男教师中选3名教师组成一个援川团队,其中a=
xdx,要求团队中男、女教师都有,则不同的组队方案种数为( )
| ∫ | 4 0 |
| 5 |
| 8 |
| A、140 | B、100 |
| C、80 | D、70 |
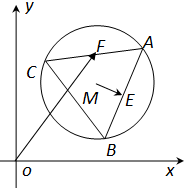 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,