题目内容
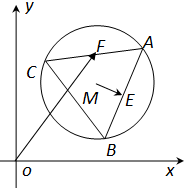 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,| ME |
| OF |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,直线与圆
分析:运用向量的三角形法则,结合向量的数量积的定义,可得
•
=-
-
•
,再由向量的数量积定义及余弦函数的值域即可得到最大值.
| ME |
| OF |
| 1 |
| 2 |
| ME |
| MO |
解答:
解:由题意可得
=
+
,
∴
•
=
•(
+
)=
•
+
•
,
∵
•
=|
|•|
|•cos120°=1×1×(-
)=-
,
∴
•
=-
+
•
=-
-
•
,
由于圆M:(x-3)2+(y-3)2=4,则圆心M(3,3),半径r=2,
则OM=3
,ME=1,
可得
•
=1×3
cos<
,
>∈[-3
,3
],
故
•
的最大值是大为3
-
.
故答案为:3
-
.
| OF |
| OM |
| MF |
∴
| ME |
| OF |
| ME |
| OM |
| MF |
| ME |
| OM |
| ME |
| MF |
∵
| ME |
| MF |
| ME |
| MF |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| ME |
| OF |
| 1 |
| 2 |
| ME |
| OM |
| 1 |
| 2 |
| ME |
| MO |
由于圆M:(x-3)2+(y-3)2=4,则圆心M(3,3),半径r=2,
则OM=3
| 2 |
可得
| ME |
| MO |
| 2 |
| ME |
| MO |
| 2 |
| 2 |
故
| ME |
| OF |
| 2 |
| 1 |
| 2 |
故答案为:3
| 2 |
| 1 |
| 2 |
点评:本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,余弦函数的值域,

练习册系列答案
相关题目
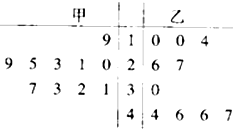 林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )
林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )| A、x甲>x乙,甲种树苗比乙种树苗高度更整齐 |
| B、x甲>x乙,乙种树苗比甲种树苗高度更整齐 |
| C、x甲<x乙,甲种树苗比乙种树苗高度更整齐 |
| D、x甲<x乙,乙种树苗比甲种树苗高度更整齐 |
为了保护环境,发展低碳经济,甲、乙两企业在国家科研部门的支持下,进行技术攻关,采用新工艺,减少二氧化碳排放量.已知从2009年6月起至2010年3月止,两企业每月的减排量如右图所示,则甲、乙两企业在这10个月内月平均减排量分别为( )
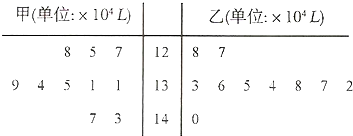

| A、133,133 |
| B、134,133 |
| C、134,134 |
| D、1343,134 |