题目内容
根据工作需要,现从4名女教师,a名男教师中选3名教师组成一个援川团队,其中a=
xdx,要求团队中男、女教师都有,则不同的组队方案种数为( )
| ∫ | 4 0 |
| 5 |
| 8 |
| A、140 | B、100 |
| C、80 | D、70 |
考点:定积分
专题:导数的综合应用
分析:首先通过定积分求出a,然后利用排列组合的知识求组队方案.
解答:
解:a=
xdx=
x2
=5,
从4名女教师,5名男教师中选3名教师组成一个援川团队,要求团队中男、女教师都有,不同的组队方案为
∵从4名女教师,5名男教师中选3名教师,要求男、女教师都有,
∴共有1个男教师2个女教师;2个男教师1个女教师两种情况,
∴共有C41C52+C42C51=40+30=70种结果,
故选D.
| ∫ | 4 0 |
| 5 |
| 8 |
| 5 |
| 16 |
| | | 4 0 |
从4名女教师,5名男教师中选3名教师组成一个援川团队,要求团队中男、女教师都有,不同的组队方案为
∵从4名女教师,5名男教师中选3名教师,要求男、女教师都有,
∴共有1个男教师2个女教师;2个男教师1个女教师两种情况,
∴共有C41C52+C42C51=40+30=70种结果,
故选D.
点评:本题考查分类加法原理,是一个常见的题目类型,这种题目关键是看清分类的标准,争取做到不重不漏,这是一个基础题,教材上有类似的题目.

练习册系列答案
相关题目
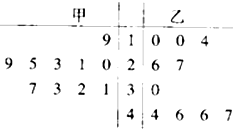 林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )
林业管理部门为了保证树苗的质量,在植物节前对所购进的树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,它们的高度用茎叶图表示如下(单位:厘米).若甲、乙两种树苗的平均高度分别是x甲,x乙,则下列结论正确的是( )| A、x甲>x乙,甲种树苗比乙种树苗高度更整齐 |
| B、x甲>x乙,乙种树苗比甲种树苗高度更整齐 |
| C、x甲<x乙,甲种树苗比乙种树苗高度更整齐 |
| D、x甲<x乙,乙种树苗比甲种树苗高度更整齐 |
已知数列{an}是等差数列,从a1,a2,a3,a4,a5,a6,a7中取走任意四项,则剩下三项构成等差数列的概率为( )
A、
| ||
B、
| ||
C、1或
| ||
D、1或
|
为了保护环境,发展低碳经济,甲、乙两企业在国家科研部门的支持下,进行技术攻关,采用新工艺,减少二氧化碳排放量.已知从2009年6月起至2010年3月止,两企业每月的减排量如右图所示,则甲、乙两企业在这10个月内月平均减排量分别为( )

| A、133,133 |
| B、134,133 |
| C、134,134 |
| D、1343,134 |
已知偶函数f(x)在[0,+∞)上为增函数,若关于x的方程f(b)=f(|2x-1|)有且只有一个实根,则实数b的取值范围是( )
| A、b≥2 |
| B、b≥0 |
| C、b≤-1或b=0 |
| D、b≥1或b≤-1或b=0 |
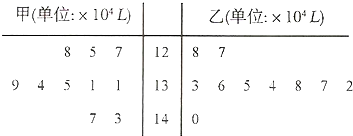
 2014年11月12日,科幻巨片《星际穿越》上映,上映至今,全球累计票房高达6亿美金.为了解绵阳观众的满意度,某影院随机调查了本市观看此影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
2014年11月12日,科幻巨片《星际穿越》上映,上映至今,全球累计票房高达6亿美金.为了解绵阳观众的满意度,某影院随机调查了本市观看此影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).