题目内容
数列{an}，满足对任意的n∈N+，均有an+an+1+an+2为定值．若a7=2，a9=3，a98=4，则数列{an}的前100项的和S100=（ ）
| A、132 | B、299 |
| C、68 | D、99 |
考点：数列的求和
专题：等差数列与等比数列
分析：对任意的n∈N+，均有an+an+1+an+2为定值，可得（an+1+an+2+an+3）-（an+an+1+an+2）=0，an+3=an，于是{an}是以3为周期的数列，即可得出．
解答：
解：对任意的n∈N+，均有an+an+1+an+2为定值，
∴（an+1+an+2+an+3）-（an+an+1+an+2）=0，
故an+3=an，
∴{an}是以3为周期的数列，
故a1=a7=2，a2=a98=4，a3=a9=3，
∴S100=（a1+a2+a3）+…+（a97+a98+a99）+a100=33（2+4+3）+a1=299．
故选：B．
∴（an+1+an+2+an+3）-（an+an+1+an+2）=0，
故an+3=an，
∴{an}是以3为周期的数列，
故a1=a7=2，a2=a98=4，a3=a9=3，
∴S100=（a1+a2+a3）+…+（a97+a98+a99）+a100=33（2+4+3）+a1=299．
故选：B．
点评：本题考查了数列的周期性，考查了计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
已知抛物线C：y2=4x，直线l过点T（t，0）且与抛物线相交于A、B两点，O为坐标原点，若∠AOB为锐角，则t的取值范围是（ ）
| A、0＜t＜4 |
| B、0＜t＜2 |
| C、t≥2 |
| D、t＞4或t＜0 |
函数f（x）的零点与g（x）=4x+2x-2的零点之差的绝对值不超过0.25，则f（x）可以是（ ）
| A、f（x）=ex-1 | ||
| B、f（x）=（x-1）2 | ||
| C、f（x）=4x-1 | ||
D、f（x）=ln（x-
|
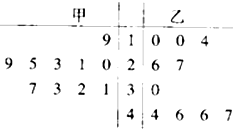林业管理部门为了保证树苗的质量，在植物节前对所购进的树苗进行检测，现从甲、乙两种树苗中各抽测了10株树苗的高度，它们的高度用茎叶图表示如下（单位：厘米）．若甲、乙两种树苗的平均高度分别是x甲，x乙，则下列结论正确的是（ ）| A、x甲＞x乙，甲种树苗比乙种树苗高度更整齐 |
| B、x甲＞x乙，乙种树苗比甲种树苗高度更整齐 |
| C、x甲＜x乙，甲种树苗比乙种树苗高度更整齐 |
| D、x甲＜x乙，乙种树苗比甲种树苗高度更整齐 |
已知数列{an}是等差数列，从a1，a2，a3，a4，a5，a6，a7中取走任意四项，则剩下三项构成等差数列的概率为（ ）
A、
| ||
B、
| ||
C、1或
| ||
D、1或
|