以点为圆心且与直线3x-4y+5=0相切的圆的方程为( )A．(x-2)2+(y+1)2=3B．(x+2)2+(y-1)2=3C．(x-2)2+(y+1)2=9D．(x+2)2+(y-1)2=9 题目和参考答案——青夏教育精英家教网—

题目内容

3．以点（2，-1）为圆心且与直线3x-4y+5=0相切的圆的方程为（　　）

A．

（x-2）²+（y+1）²=3

B．

（x+2）²+（y-1）²=3

C．

（x-2）²+（y+1）²=9

D．

（x+2）²+（y-1）²=9

分析圆的半径为圆心到直线的距离，从而得出答案．

解答解：∵圆与直线3x-4y+5=0相切，
∴圆的半径r=$\frac{|6+4+5|}{\sqrt{9+16}}$=3，
∴圆的方程为：（x-2）²+（y+1）²=9．
故选C．

点评本题考查了圆的标准方程，直线与圆的位置关系，属于中档题．

练习册系列答案

14．设集合A={-1，0，1，2}，B={x|-2≤x≤1}，则A∩B=（　　）

11．已知函数f（x）=lnx+ax在点（t，f（t））处的切线方程为y=3x+1
（1）求a的值；
（2）已知k≤2，当x＞1时，f（x）＞k（1-$\frac{3}{x}$）+2x-1恒成立，求实数k的取值范围；
（3）对于在（0，1）中的任意一个常数b，是否存在正数x₀，使得e${\;}^{f（{x}_{0}+1）-3{x}_{0}-2}$+$\frac{b}{2}$x₀²＜1？请说明理由．

18．已知函数f（x）=$\frac{1}{x}$，以下关于函数f（x）的判断中正确的是（　　）

	A．	f（x）是偶函数，在（0，+∞）内是增函数		B．	f（x）是偶函数，在（0，+∞）内是减函数
	C．	f（x）是奇函数，在（0，+∞）内是增函数		D．	f（x）是奇函数，在（0，+∞）内是减函数

8．某高新技术公司要生产一批新研发的A款手机和B款手机，生产一台A款手机需要甲材料3kg，乙材料1kg，并且需要花费1天时间，生产一台B款手机需要甲材料1kg，乙材料3kg，也需要1天时间，已知生产一台A款手机利润是1000元，生产一台B款手机的利润是2000元，公司目前有甲、乙材料各，则在300kg不超过120天的情况下，公司生产两款手机的最大利润是210000元．

15．在平面直角坐标系xOy中，已知双曲线的渐近线方程为y=±x，且它的一个焦点与抛物线x²=8y的焦点重合，则该双曲线的方程为$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{2}=1$．

12．数列{a_n}中，a_2n=a_2n-1+（-1）ⁿ，a_2n+1=a_2n+n，a₁=1则a₁₀₀=1226．

13．某校为了解学生对数学学案质量的满意度，从高一、高二两个年级分别随机调查了20个学生，得到对学案满意度评分（满分100分）的茎叶图如图：则下列说法错误的是（　　）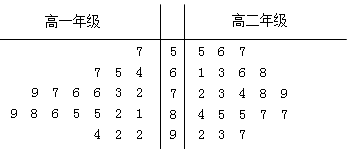

	A．	高一学生满意度评分的平均值比高二学生满意度评分的平均值高
	B．	高一学生满意度评分比较集中，高二学生满意度评分比较分散
	C．	高一学生满意度评分的中位数为80
	D．	高二学生满意度评分的中位数为74

试题分类