题目内容
15.在平面直角坐标系xOy中,已知双曲线的渐近线方程为y=±x,且它的一个焦点与抛物线x2=8y的焦点重合,则该双曲线的方程为$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{2}=1$.分析 清楚抛物线的焦点坐标,得到双曲线的焦点坐标,利用双曲线的渐近线方程求解双曲线方程即可.
解答 解:抛物线x2=8y的焦点坐标(0,2),双曲线的渐近线方程为y=±x,且它的一个焦点与抛物线x2=8y的焦点重合,所以双曲线的实轴在y轴,双曲线设为y2-x2=m,m>0,
$\sqrt{2m}=2$,解得m=2,
所求的双曲线方程为:$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{2}=1$.
故答案为:$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{2}=1$.
点评 本题考查双曲线的简单性质以及抛物线的简单性质的应用,考查计算能力、

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设i是虚数单位,复数z满足z•(1+$\sqrt{2}$i)=-$\sqrt{2}$i,则复数z的虚部等于( )
| A. | -$\frac{\sqrt{2}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | -$\frac{2}{3}$ |
6.已知双曲线C的中心在原点,焦点在y轴上,若双曲线C的一条渐近线与直线$\sqrt{2}$x-y-1=0平行,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
3.以点(2,-1)为圆心且与直线3x-4y+5=0相切的圆的方程为( )
| A. | (x-2)2+(y+1)2=3 | B. | (x+2)2+(y-1)2=3 | C. | (x-2)2+(y+1)2=9 | D. | (x+2)2+(y-1)2=9 |
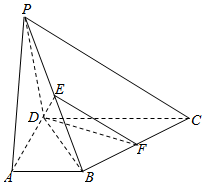 在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.
在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.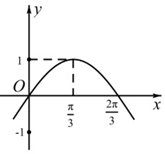 已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )
已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( ) 如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.