题目内容
18．已知函数f（x）=$\frac{1}{x}$，以下关于函数f（x）的判断中正确的是（ ）| A． | f（x）是偶函数，在（0，+∞）内是增函数 | B． | f（x）是偶函数，在（0，+∞）内是减函数 | ||
| C． | f（x）是奇函数，在（0，+∞）内是增函数 | D． | f（x）是奇函数，在（0，+∞）内是减函数 |
分析 根据反比例函数的性质进行判断即可．
解答 解：函数的定义域为（-∞，0）∪（0，+∞），
f（-x）=-$\frac{1}{x}$=-f（x），则函数f（x）是奇函数，
则（0，+∞）上为减函数，
故选：D
点评 本题主要考查函数奇偶性和单调性的判断，结合反比例函数的性质是解决本题的关键．
练习册系列答案
相关题目
8．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$，过点F（c，0）作直线交双曲线C的两条渐近线于A，B两点，若B为FA的中点，且OA=c，则双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | $2\sqrt{3}$ | D． | $4\sqrt{3}$ |
6．已知双曲线C的中心在原点，焦点在y轴上，若双曲线C的一条渐近线与直线$\sqrt{2}$x-y-1=0平行，则双曲线C的离心率为（ ）
| A． | $\frac{\sqrt{6}}{2}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
13．“=”在基本算法语句中叫（ ）
| A． | 赋值号 | B． | 等号 | C． | 输入语句 | D． | 输出语句 |
3．以点（2，-1）为圆心且与直线3x-4y+5=0相切的圆的方程为（ ）
| A． | （x-2）2+（y+1）2=3 | B． | （x+2）2+（y-1）2=3 | C． | （x-2）2+（y+1）2=9 | D． | （x+2）2+（y-1）2=9 |
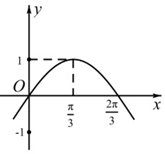已知函数f（x）=Asin（ωx+$\frac{π}{6}$）-1（A＞0，ω＞0）的部分图象如图，则对于区间[0，π]内的任意实数x1，x2，f（x1）-f（x2）的最大值为（ ）