��Ŀ����
8��ij���¼�����˾Ҫ����һ�����з���A���ֻ���B���ֻ�������һ̨A���ֻ���Ҫ�ײ���3kg���Ҳ���1kg��������Ҫ����1��ʱ�䣬����һ̨B���ֻ���Ҫ�ײ���1kg���Ҳ���3kg��Ҳ��Ҫ1��ʱ�䣬��֪����һ̨A���ֻ�������1000Ԫ������һ̨B���ֻ���������2000Ԫ����˾Ŀǰ�мס��Ҳ��ϸ�������300kg������120�������£���˾���������ֻ������������210000Ԫ������ ������A���ֻ�x̨��B���ֻ�y̨�������ܺ�Ϊz���ó�Լ��������ʾ�Ŀ������ݿ�����ó�Ŀ�꺯��ȡ�����ֵʱ�����Ž⣮
���  �⣺������A���ֻ�x̨��B���ֻ�y̨�������ܺ�Ϊz��
�⣺������A���ֻ�x̨��B���ֻ�y̨�������ܺ�Ϊz��
��$\left\{\begin{array}{l}{3x+y��300}\\{x+3y��300}\\{x+y��120}\\{x��0��y��0}\end{array}\right.$��Ŀ�꺯��z=1000x+2000y��
������������ͼ��ʾ��
��z=1000x+2000������y=-$\frac{1}{2}$x+$\frac{z}{2000}$��
��ͼ���֪����ֱ�߾�����Mʱ��zȡ�����ֵ��
�ⷽ����$\left\{\begin{array}{l}{x+3y=300}\\{x+y=120}\end{array}\right.$����M������Ϊ��30��90����
���Ե�x=30��y=90ʱ��zmax=1000��30+2000��90=210000��
��������ƷA����ƷB������֮�͵����ֵΪ210000Ԫ��
���� ���⿼���˼����Թ滮��Ӧ�ã�����Լ�����������ݿ������ж����Ž��λ���ǹؼ��������е��⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
18�����������ABC�����߳�a��b��c�ɵȲ����У���a2+b2+c2=21����ʵ��b��ȡֵ��Χ�ǣ�������
| A�� | $��{\sqrt{6}��\sqrt{7}}]$ | B�� | $��{0��\sqrt{7}}]$ | C�� | $��{\frac{{2\sqrt{42}}}{5}��\sqrt{7}}]$ | D�� | ��6��7] |
19������{an}�У�������ak��ʹ�á�ak��ak-1��ak��ak+1������������k��2��k��N*����ak���Ϊ{an}��һ��Hֵ�������������У�
��an=1-2n
��an=sinn
��an=$\frac{n-2}{{e}^{n-3}}$
��an=lnn-n
�����Hֵ�����е����Ϊ��������
��an=1-2n
��an=sinn
��an=$\frac{n-2}{{e}^{n-3}}$
��an=lnn-n
�����Hֵ�����е����Ϊ��������
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ۢ� |
16��${log_2}8+{log_2}\frac{1}{2}$=��������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
3���Ե㣨2��-1��ΪԲ������ֱ��3x-4y+5=0���е�Բ�ķ���Ϊ��������
| A�� | ��x-2��2+��y+1��2=3 | B�� | ��x+2��2+��y-1��2=3 | C�� | ��x-2��2+��y+1��2=9 | D�� | ��x+2��2+��y-1��2=9 |
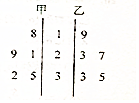 �ס����������ݵľ�Ҷͼ��ͼ��ʾ����ƽ������С��һ����Ϊ�ף���ѡ��ס����ҡ���
�ס����������ݵľ�Ҷͼ��ͼ��ʾ����ƽ������С��һ����Ϊ�ף���ѡ��ס����ҡ���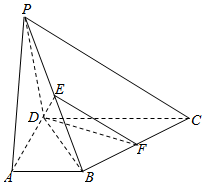 ������P-ABCD�У�����ABCDΪֱ�����Σ���BAD=��ADC=90�㣬DC=2AB=2AD��BC��PD��E��F�ֱ���PB��BC���е㣮
������P-ABCD�У�����ABCDΪֱ�����Σ���BAD=��ADC=90�㣬DC=2AB=2AD��BC��PD��E��F�ֱ���PB��BC���е㣮