题目内容
已知集合M={x|mx+1-
=0,x∈R},若M=∅,则实数m的取值范围是 .
| x-3 |
考点:集合的相等
专题:计算题,集合
分析:由题意,方程mx+1-
=0无解,令
=t(t≥0),则x=t2+3,则m(t2+3)+1-t=0在[0,+∞)上无解.讨论m,确定方程在[0,+∞)上无解时m的取值范围.
| x-3 |
| x-3 |
解答:
解:由题意,方程mx+1-
=0无解,
令
=t(t≥0),则x=t2+3,则
m(t2+3)+1-t=0在[0,+∞)上无解.
即mt2-t+1+3m=0,
则若m=0,方程有解.
若m<0,则1+3m<0,则m<-
,
若m>0,则△=1-m(1+3m)<0或
,
解得,m>
,
故答案为:m<-
或m>
.
| x-3 |
令
| x-3 |
m(t2+3)+1-t=0在[0,+∞)上无解.
即mt2-t+1+3m=0,
则若m=0,方程有解.
若m<0,则1+3m<0,则m<-
| 1 |
| 3 |
若m>0,则△=1-m(1+3m)<0或
|
解得,m>
-1+
| ||
| 6 |
故答案为:m<-
| 1 |
| 3 |
-1+
| ||
| 6 |
点评:本题考查了集合相等的应用,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
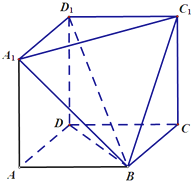 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.