题目内容
已知数列{an}满足a1=1,an+1=an+n+1,求数列{an}的通项公式.
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:根据已知数列{an}满足an+1=an+n+1,移项即可发现规律an+1-an是一个等差数列,即可得出结论.
解答:
解:由an+1=an+n+1得an+1-an=n+1则
n≥2,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+…+2+1+1
=
+1
所以数列{an}的通项公式为an=
.
n≥2,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+…+2+1+1
=
| n(n+1) |
| 2 |
所以数列{an}的通项公式为an=
|
点评:本题主要考查由递推公式推导数列的通项公式,通过变形我们要发现数列的规律,转化到等差或等比数列上来,就会很容易解决问题.

练习册系列答案
相关题目
棱长为a的正方体,过上底面两邻边中点和下底面中心作截面,则截面图形的周长是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知集合M中含有3个元素:0,x2,-x,则x满足的条件是( )
| A、x≠0 |
| B、x≠-1 |
| C、x≠0且x≠-1 |
| D、x≠0且x≠1 |
已知四面体P-ABC中,PA=4,AC=2
,PB=PC=2
,PA⊥平面PBC,则四面体P-ABC的内切球半径与外接球半径的比( )
| 7 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
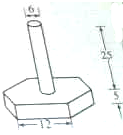 如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).
如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).