题目内容
已知函数f(x)=x2-(m+1)x+m(m∈R).
(1)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(2)若tanA,tanB是方程f(x)+4=0的两个实根,A,B是锐角三角形的两个内角,求证:m≥5.
(1)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(2)若tanA,tanB是方程f(x)+4=0的两个实根,A,B是锐角三角形的两个内角,求证:m≥5.
考点:两角和与差的正切函数,二次函数的性质
专题:三角函数的求值
分析:(1)利用对任意实数α,恒有f(2+cosα)≤0,结合余弦函数的范围,推出不等式,求出x的最大值,即可证明m≥3;
(2)利用韦达定理以及若tanA,tanB是方程f(x)+4=0的两个实根,A,B是锐角三角形的两个内角,推出A+B的范围,得到m的不等式组,求出m的范围,即可证明m≥5.
(2)利用韦达定理以及若tanA,tanB是方程f(x)+4=0的两个实根,A,B是锐角三角形的两个内角,推出A+B的范围,得到m的不等式组,求出m的范围,即可证明m≥5.
解答:
(1)证明:∵f(x)=x2-(m+1)x+m=(x-1)(x-m),
又-1≤cosα≤1,
∴1≤2+cosα≤3,恒有f(2+cosα)≤0,
即1≤x≤3时,恒有f(x)≤0,
即:(x-1)(x-m)≤0,
∴m≥x,又xmax=3,
故m≥3.
(2)证明:f(x)+4=0,即x2-(m+1)x+m+4=0,
由题意可得:
又A、B为锐角三角形的两个内角,
∴
<A+B<π.
∴tan(A+B)<0,tan(A+B)=
=
<0.
因而
,
解得m≥5.
又-1≤cosα≤1,
∴1≤2+cosα≤3,恒有f(2+cosα)≤0,
即1≤x≤3时,恒有f(x)≤0,
即:(x-1)(x-m)≤0,
∴m≥x,又xmax=3,
故m≥3.
(2)证明:f(x)+4=0,即x2-(m+1)x+m+4=0,
由题意可得:
|
又A、B为锐角三角形的两个内角,
∴
| π |
| 2 |
∴tan(A+B)<0,tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
| m+1 |
| -m-3 |
因而
|
解得m≥5.
点评:本题考查两角和与差的三角函数,三角函数的最值的求法,函数恒成立的应用,考查计算能力.

练习册系列答案
相关题目
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知x>0,y>0,且2x+y=1,则
+
的最小值为( )
| 1 |
| x |
| 1 |
| y |
| A、3 | ||
B、2+3
| ||
C、3+2
| ||
D、2-3
|
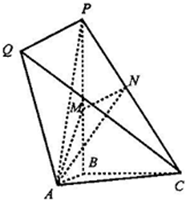 如图所示的几何体中,PB⊥面ABC,PQ∥AB,PQ=PB=1;Rt△ABC中,∠ABC=90°,AB=BC=
如图所示的几何体中,PB⊥面ABC,PQ∥AB,PQ=PB=1;Rt△ABC中,∠ABC=90°,AB=BC=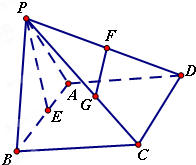 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.