题目内容
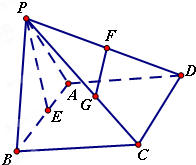 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.(1)求证:FG∥平面PAB;
(2)求证:平面PEC⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:作图题,证明题,空间位置关系与距离
分析:(1)由中位线说明线线平行,由平行线的传递性说明线线平行,进而说明线面平行;(2)构造等边三角形,说明垂直,从而由线面垂直判定定理说明线面垂直,进而证明面面垂直.
解答:
证明:(1)、∵F、G分别是PD、PC的中点,
∴FG∥DC,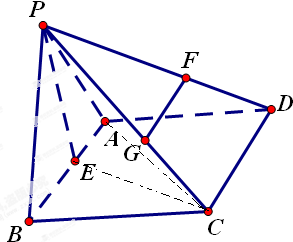
又∵AB∥DC,
∴FG∥AB,又∵AB?平面PAB,FG?平面PAB,
∴FG∥平面PAB.
(2)、连接PE、CE、AC,
∵AB=BC,∠ABC=60°,
∴△ABC为等边三角形,又∵E是AB的中点,
∴CE⊥AB,同理PE⊥AB,
∴AB⊥平面PEC,又∵AB∥DC,
∴DC⊥平面PEC,
∴平面PEC⊥平面PCD.
∴FG∥DC,

又∵AB∥DC,
∴FG∥AB,又∵AB?平面PAB,FG?平面PAB,
∴FG∥平面PAB.
(2)、连接PE、CE、AC,
∵AB=BC,∠ABC=60°,
∴△ABC为等边三角形,又∵E是AB的中点,
∴CE⊥AB,同理PE⊥AB,
∴AB⊥平面PEC,又∵AB∥DC,
∴DC⊥平面PEC,
∴平面PEC⊥平面PCD.
点评:本题考查了线面平行,面面垂直的判定定理,同时考查了平行线的传递性,中位线说明平行,构造等边三角形证明垂直及线面垂直的判定等,考查的综合性较强,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
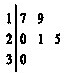 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
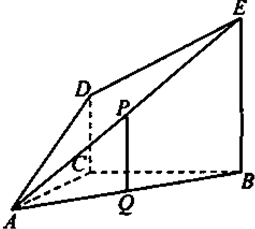
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,cos∠ADB=
如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,cos∠ADB=