题目内容

若a，b，c＞0，求证：
（Ⅰ）
a2+b2
ab
+
b2+c2
bc
+
c2+a2
ca
≥6；   
（Ⅱ）
a+b
2
•
b+c
2
•
c+a
2
≥abc．
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：（Ⅰ）利用基本不等式，再相加即可证明结论；
（Ⅱ）利用基本不等式，再相乘即可证明结论．
解答： 证明：（Ⅰ）∵a，b，c＞0，
∴
a2+b2
ab
+
b2+c2
bc
+
c2+a2
ca
≥
2ab
ab
+
2bc
bc
+
2ca
ca
=2+2+2=6，
即
a2+b2
ab
+
b2+c2
bc
+
c2+a2
ca
≥6．     
（Ⅱ）
a+b
2
•
b+c
2
•
c+a
2
≥
2
ab
2
•
2
bc
2
•
2
ca
2
=
ab
•
bc
•
ca
=abc，
即
a+b
2
•
b+c
2
•
c+a
2
≥abc．
点评：本题考察了均值定理a2+b2≥2ab的应用，及不等式的基本性质的应用，属基础题
练习册系列答案
相关题目
已知向量
a
=（1，2），
b
=（2，-3），
c
=（1，x），若向量
c
满足
c
⊥（
a
+
b
），则x=（　　）
A、4B、2C、3D、6
从装有红球、白球和黑球各2个的口袋内一次取出2个球，给出以下事件：
①两球都不是白球；
②两球中恰有一白球；
③两球中至少有一个白球．
其中与事件“两球都为白球”互斥而非对立的事件是（　　）
A、①②B、①③C、②③D、①②③
已知函数f（x）=cos（2x-
π
3
）+2sin（x-
π
4
）sin（x+
π
4
）．
（Ⅰ）求函数f（x）的最小正周期和图象的对称轴方程；
（Ⅱ）求函数f（x）在区间[-
π
12
，
π
2
]上的值域；
（Ⅲ） 令g（x）=f（x-
π
6
），判断函数g（x）的奇偶性，并说明理由．
已知函数f（x）=x2-（m+1）x+m（m∈R）．
（1）对任意实数α，恒有f（2+cosα）≤0，证明m≥3；
（2）若tanA，tanB是方程f（x）+4=0的两个实根，A，B是锐角三角形的两个内角，求证：m≥5．
已知函数f（x）=
1
3
x3+
1
2
ax2-（a+2）x+b（a，b∈R）在[-1，1]上是减函数．
（1）求实数a的取值范围；
（2）设
1
2
＜a＜1，若对任意实数u、v∈[a-1，a]，不等式|f（u）-f（v）|≤
29
12
恒成立，求实数a的最小值．
求与圆A：（x-5）2+y2=49和圆B：（x+5）2+y2=1都外切的圆心P的轨迹方程．
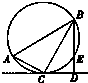如图，在△ABC中，∠ACB=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，求DE的长．
如图，△ABC的外接圆⊙O的半径为5，CE垂直于⊙O所在的平面，BD∥CE，CE=4，BC=6，且BD=1，cos∠ADB=
101
101
．
（1）求证：平面AEC⊥平面BCED；
（2）试问线段DE上是否存在点M，使得直线AM与平面ACE所成角的正弦值为
2
21
21
？若存在，确定点M的位置；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网