题目内容
已知z=1+i，如果z2+az+b=（1-i）（1-z），求实数a、b的值．
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：代入化简等式两边的复数，由复数相等可得a、b的方程组，解方程组即可．
解答：
解：∵z=1+i，∴z2+az+b
=（1+i）2+a（1+i）+b
=a+b+（a+2）i
同理可得（1-i）（1-z）
=-（1-i）i=-1-i，
又z2+az+b=（1-i）（1-z），
∴a+b+（a+2）i=-1-i
∴
，解得
=（1+i）2+a（1+i）+b
=a+b+（a+2）i
同理可得（1-i）（1-z）
=-（1-i）i=-1-i，
又z2+az+b=（1-i）（1-z），
∴a+b+（a+2）i=-1-i
∴
|
|
点评：本题考查复数代数形式的运算，涉及复数相等，属基础题．
练习册系列答案
相关题目
已知△ABC中，a=4，b=4
，∠A=30°则∠B等于（ ）
| 3 |
| A、300 |
| B、600 |
| C、300或1500 |
| D、600或 1200 |
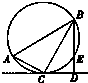如图，在△ABC中，∠ACB=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，求DE的长．