题目内容
在△ABC中,a,b,c分别是角A,B,C所对的边,已知a=
,b=3,c=30°,则A= .
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:根据余弦定理好条件求出c的长度,然后根据条件即可求出A的角度.
解答:
解:由题意得△ABC中,a=
,b=3,C=30°,
由余弦定理得:c2=a2+b2-2abcosC=3+9-9=3,
则c=
,
所以a=c,则A=C=30°,
故答案为:30°.
| 3 |
由余弦定理得:c2=a2+b2-2abcosC=3+9-9=3,
则c=
| 3 |
所以a=c,则A=C=30°,
故答案为:30°.
点评:本题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
从6名志愿者中选出4人,分别从事搜救、医疗、心理辅导、后勤四种不同工作,若其中甲、乙两名志愿者都不能从事心理辅导工作,则不同的选派方案共有( )
| A、96种 | B、180种 |
| C、240种 | D、280种 |
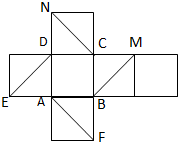 如图,为正方体的平面展开图,在这个正方体中
如图,为正方体的平面展开图,在这个正方体中