题目内容
若对任意x∈R,不等式
>sinθ-1恒成立,求θ的取值范围.
| (x2+1)cosθ-x(cosθ-5)+3 |
| x2-x+1 |
考点:函数恒成立问题
专题:计算题,函数的性质及应用
分析:原不等式变形为:(cosθ-sinθ+1)x2-(cosθ-sinθ-4)x+cosθ-sinθ+4>0,令t=cosθ-sinθ得:(t+1)x2-(t-4)x+t+4>0,求出t的范围,即可求θ的取值范围.
解答:
解:原不等式变形为:(cosθ-sinθ+1)x2-(cosθ-sinθ-4)x+cosθ-sinθ+4>0
令t=cosθ-sinθ得:(t+1)x2-(t-4)x+t+4>0,
∴
⇒t>0
∴cosθ-sinθ>0,∴cosθ>sinθ,∴2kπ-
<θ<2kπ+
,k∈Z
所以θ得范围是(2kπ-
,2kπ+
) k∈Z
令t=cosθ-sinθ得:(t+1)x2-(t-4)x+t+4>0,
∴
|
∴cosθ-sinθ>0,∴cosθ>sinθ,∴2kπ-
| 3π |
| 4 |
| π |
| 4 |
所以θ得范围是(2kπ-
| 3π |
| 4 |
| π |
| 4 |
点评:本小题主要考查函数恒成立问题、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
已知
=1-ni,其中m,n∈R,i为虚数 单位,则m+ni=( )
| m |
| 1+i |
| A、1+2i | B、2+i |
| C、1-2i | D、2-i |
若函数f(x),g(x)分别是定义在实数集R上的奇函数、偶函数,且满足f(x)-g(x)=ex(e是自然对数的底数),则有( )
| A、f(2)<f(3)<g(0) |
| B、g(0)<f(3)<f(2) |
| C、g(0)<f(2)<f(3) |
| D、f(2)<g(0)<f(3) |
已知(2,1)是直线l被椭圆
+
=1所截得的线段的中点,则直线l的方程是( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、x+2y-4=0 |
| B、x-2y=0 |
| C、x+8y-10=0 |
| D、x-8y+6=0 |
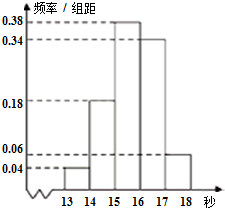 高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.