题目内容

等比数列{an}中，an＞0，q≠1，且a2、
1
2
a3、a1成等差数列，则
a14+a17
a12+a15
=
 
．
考点：等比关系的确定
专题：等差数列与等比数列
分析：利用等差数列由等比数列的通项公式及其性质即可得出．
解答： 解：∵a2、
1
2
a3、a1成等差数列，
∴a3=a2+a1．
∵数列{an}是等比数列{an}．
∴a1q2=a1q+a1，
化为q2-q-1=0，q＞0，q≠1．
解得q=
1+
5
2
．
∴
a14+a17
a12+a15
=
a12q2+a15q2
a12+a15
=q2=
3+
5
2
．
故答案为：
3+
5
2
．
点评：本题考查了等差数列由等比数列的通项公式及其性质，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x2-2lnx，h（x）=x2-x+a．
（1）其求函数f（x）的极值；
（2）设函数k（x）=f（x）-g（x），若函数k（x）在[1，3]上恰有两个不同零点求实数a的取值范围．
已知函数f （x）=ax-ln x（a∈R）．
（Ⅰ）求f （x）的单调区间；
（Ⅱ）当a＞0时，求f （x）在区间（0，e]上的最小值．
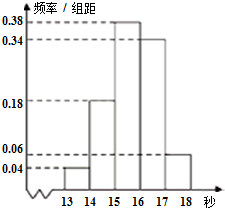高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
（1）若成绩在区间[14，16）内规定为良好，求该班在这次百米测试中成绩为良好的人数；
（2）请根据频率分布直方图估计样本数据的众数和中位数（精确到0.01）．
已知变量x，y满足约束条件
x+y≥1
y≤4
x-y≤1
，若z=kx+y的最大值为5，则实数k=
 
．
函数y=lg（sinx-cosx-1）的定义域为
 
．
已知函数f（x）=e-x-
1
2
（x＞0）与g（x）=ln（x+a）的图象有交点，则a的取值范围是（　　）
A、(-∞，
e
)
B、(-∞，
1
e
)
C、(-
1
e
，
e
)
D、(-
e
，
1
e
)
给出命题p：a（a-1）＜0；命题q：y=x2+（2a-3）x+1与x轴交于不同的两点．如果命题“p∨q”为真，“p∧q”为假，求a的取值范围．
如果程序框图的输出结果是6，那么在判断框中①表示的“条件”应该是（　　）
A、i≥3B、i≥4
C、i≥5D、i≥6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网