题目内容
已知函数f(x)=(2cos2x+sin2x)tanx-1.
(1)求函数f(x)的定义域和最小正周期;
(2)当x∈[-
,0]时,求函数f(x)的最大值和最小值.
(1)求函数f(x)的定义域和最小正周期;
(2)当x∈[-
| 3π |
| 8 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,三角函数的最值
专题:三角函数的图像与性质
分析:(1)首先,根据正切函数的定义域,确定该函数的定义域,然后,借助于二倍角公式,化简函数解析式,f(x)=
sin(2x-
),然后确定该函数的周期即可;
(2)根据(1)和x∈[-
,0],结合三角函数的单调性进行求解.
| 2 |
| π |
| 4 |
(2)根据(1)和x∈[-
| 3π |
| 8 |
解答:
解:(1)∵f(x)=(2cos2x+sin2x)tanx-1
∴x≠
+kπ,k∈Z,
∴函数的定义域为:{x|x≠
+kπ,k∈Z},
∵f(x)=(2cos2x+sin2x)tanx-1
=2cos2xtanx+sin2xtanx-1
=2cosxsinx+2sin2x-1
=sin2x-cos2x
=
sin(2x-
)
∴f(x)=
sin(2x-
)
∴T=
=π,
∴函数f(x)的最小正周期π.
(2)∵x∈[-
,0],
∴-
≤2x≤0,
∴-π≤2x-
≤-
,
∴sin(2x-
)∈[-1,0],
∴f(x)=
sin(2x-
)∈[-
,0],
∴最小值-
;最大值0.
∴x≠
| π |
| 2 |
∴函数的定义域为:{x|x≠
| π |
| 2 |
∵f(x)=(2cos2x+sin2x)tanx-1
=2cos2xtanx+sin2xtanx-1
=2cosxsinx+2sin2x-1
=sin2x-cos2x
=
| 2 |
| π |
| 4 |
∴f(x)=
| 2 |
| π |
| 4 |
∴T=
| 2π |
| 2 |
∴函数f(x)的最小正周期π.
(2)∵x∈[-
| 3π |
| 8 |
∴-
| 3π |
| 4 |
∴-π≤2x-
| π |
| 4 |
| π |
| 4 |
∴sin(2x-
| π |
| 4 |
∴f(x)=
| 2 |
| π |
| 4 |
| 2 |
∴最小值-
| 2 |
点评:本题重点考查了三角函数的图象与性质、周期公式、三角恒等变换等知识,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
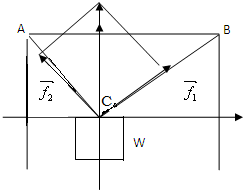 物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.
物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.