题目内容
如果不等式x2＜|x-1|+a的解集是区间（-3，3）的子集，则实数a的取值范围是 ．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：将不等式转化为函数，利用函数根与不等式解之间的关系即可得到结论．
解答：
解：不等式x2＜|x-1|+a等价为x2-|x-1|-a＜0，
设f（x）=x2-|x-1|-a，
若不等式x2＜|x-1|+a的解集是区间（-3，3）的子集，
则
，
即
，
则
，
解得a≤5，
故答案为：（-∞，5]
设f（x）=x2-|x-1|-a，
若不等式x2＜|x-1|+a的解集是区间（-3，3）的子集，
则
|
即
|
则
|
解得a≤5，
故答案为：（-∞，5]
点评：本题主要考查不等式的应用，利用不等式和函数之间的关系，转化为函数是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知如图所示的流程图（未完成），设当箭头a指向①时输出的结果S=m，当箭头a指向②时，输出的结果S=n，求m+n的值．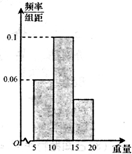
如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为某程序框图如图所示，该程序运行后输出的S为（ ）
A、-
| ||
| B、2 | ||
| C、-3 | ||
D、
|