题目内容
已知数列{an},满足a1=1,an+1=2an+1(n∈N*)
(Ⅰ)证明数列{an+1}是等比数列
(Ⅱ)若数列{bn}满足4 b1-1•42b2-1•4 3b3-1…4 nbn-1=(an+1)n,求数列{bn}的通项公式.
(Ⅰ)证明数列{an+1}是等比数列
(Ⅱ)若数列{bn}满足4 b1-1•42b2-1•4 3b3-1…4 nbn-1=(an+1)n,求数列{bn}的通项公式.
考点:数列递推式,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)根据等比数列的定义即可证明数列{an+1}是等比数列.
(Ⅱ)根据数列的递推关系,进行化简即可得到结论.
(Ⅱ)根据数列的递推关系,进行化简即可得到结论.
解答:
解:(Ⅰ)∵an+1=2an+1,
∴1+an+1=2an+2=2(an+1),
故数列{an+1}是等比数列,公比q=2,首项为2.
且an+1=2•2n-1=2n.
(Ⅱ)∵4 b1-1•42b2-1•4 3b3-1…4 nbn-1=(an+1)n,
∴4b1+2b2+…+nbn-n=(2n)n=2n2,
即2(b1+2b2+3b3+…+nbn)-2n=n2,
∴2(b1+2b2+3b3+…+nbn)=n2+2n,①
当n≥2时,2(b1+2b2+3b3+…+(n-1)bn-1)=(n-1)2+2(n-1)=n2-1,②
两式相减得2nbn=2n+1,(n≥2),
即bn=1+
,(n≥2),
当n=1时,也满足条件,故bn=1+
,(n≥1).
∴1+an+1=2an+2=2(an+1),
故数列{an+1}是等比数列,公比q=2,首项为2.
且an+1=2•2n-1=2n.
(Ⅱ)∵4 b1-1•42b2-1•4 3b3-1…4 nbn-1=(an+1)n,
∴4b1+2b2+…+nbn-n=(2n)n=2n2,
即2(b1+2b2+3b3+…+nbn)-2n=n2,
∴2(b1+2b2+3b3+…+nbn)=n2+2n,①
当n≥2时,2(b1+2b2+3b3+…+(n-1)bn-1)=(n-1)2+2(n-1)=n2-1,②
两式相减得2nbn=2n+1,(n≥2),
即bn=1+
| 1 |
| 2n |
当n=1时,也满足条件,故bn=1+
| 1 |
| 2n |
点评:本题主要考查等比数列的证明和判断,利用递推数列是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
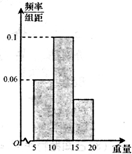 如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为
如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为