题目内容
16.从1,2,3,4这四个数中一次随机抽取两个数,则取出的数中一个是奇数一个是偶数的概率为$\frac{2}{3}$.分析 从1,2,3,4这四个数中一次随机抽取两个数,先求出基本事件总数,再求出取出的数中一个是奇数一个包含的基本事件个数,由此能求出取出的数中一个是奇数一个是偶数的概率.
解答 解:从1,2,3,4这四个数中一次随机抽取两个数,
基本事件总数n=${C}_{4}^{2}$=6,
取出的数中一个是奇数一个包含的基本事件个数m=${C}_{2}^{1}{C}_{2}^{1}$=4,
∴取出的数中一个是奇数一个是偶数的概率p=$\frac{m}{n}$=$\frac{4}{6}=\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
6.已知一次函数f(x)=ax-1满足a∈[-1,2]且a≠0,那么对于a,使得f(x)≤0在x∈[0,1]上成立的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.变量x,y具有线性相关关系,现测得一组数据如下:
根据如表,利用最小二乘法得到回归直线方程$\stackrel{∧}{y}$=0.7x+0.55,据此判断,当x=5,时,$\stackrel{∧}{y}$与实际值y的大小关系为( )
| x | 2 | 3 | 4 | 5 |
| y | 2 | 2.5 | 3.5 | 4 |
| A. | $\stackrel{∧}{y}$>y | B. | $\stackrel{∧}{y}$>y | C. | $\stackrel{∧}{y}$=y | D. | 无法确定 |
11.直线x+2y-2=0与直线3x+ay+b=0之间的距离为$\sqrt{5}$,则实数b=( )
| A. | 9 | B. | -21 | C. | 9或-21 | D. | 3或7 |
1.若函数f(x)=x1g(mx+$\sqrt{{x}^{2}+1}$)为偶函数,则m=( )
| A. | -1 | B. | 1 | C. | -1或1 | D. | 0 |
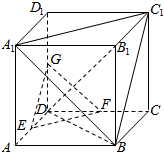 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.