题目内容
 已知ABCD为矩形,平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,M,N分别是AB,PC中点.求证:MN⊥AB.
已知ABCD为矩形,平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,M,N分别是AB,PC中点.求证:MN⊥AB.考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:由面面垂直的性质得到PA,AB,AD两两垂直,进一步证明AB垂直平面MNK即可.
解答:
证明:∵ABCD为矩形,平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,
∴AD⊥平面PAB,∴AD⊥PA;AB⊥平面PAD,∴AB⊥PA,
∵M,N分别是AB,PC中点.过M作MK∥BC,则K为PC的中点,连接NK,则NK∥PA,
∴MK⊥AB,NK⊥AB,
∴AB⊥平面MNK.
∴AB⊥MN.即MN⊥AB.
∴AD⊥平面PAB,∴AD⊥PA;AB⊥平面PAD,∴AB⊥PA,
∵M,N分别是AB,PC中点.过M作MK∥BC,则K为PC的中点,连接NK,则NK∥PA,
∴MK⊥AB,NK⊥AB,
∴AB⊥平面MNK.
∴AB⊥MN.即MN⊥AB.
点评:本题考查了面面垂直的性质以及线面垂直的判定和性质定理的运用,关键是将面面垂直、线面垂直转化为线线垂直.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
如果曲线C上任意一点的坐标都是方程F(x,y)=0的解,那么下列命题正确的是( )
| A、曲线C的方程是F(x,y)=0 |
| B、曲线C上的点都在方程F(x,y)=0的曲线上 |
| C、方程F(x,y)=0的曲线是C |
| D、以方程F(x,y)=0解为坐标点都在曲线C上 |
命题甲:若x,y∈R,则|x|>1是x>1是充分而不必要条件;命题乙:函数y=
的定义域是(-∞,-1]∪[3,+∞),则( )
| |x-1|-2 |
| A、“甲或乙”为假 |
| B、“甲且乙”为真 |
| C、甲真乙假 |
| D、甲假乙真 |
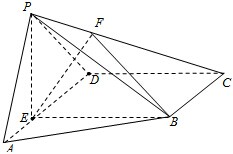 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.