题目内容
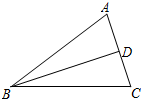 在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC=
在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC=| 1 |
| 5 |
(Ⅰ) 若BC=2,求sin∠ACB的值;
(Ⅱ) 若D是边AC中点,且BD=
| 7 |
| 2 |
考点:余弦定理的应用
专题:解三角形
分析:(Ⅰ)直接利用余弦定理求出AC,然后利用正弦定理求sin∠ACB的值;
(Ⅱ)以BA,BC为邻边作如图所示的平行四边形ABCE,如图,若D是边AC中点,且BD=
,在△BCE中,由余弦定理求出CB,在△ABC中,利用余弦定理求边AC的长.
(Ⅱ)以BA,BC为邻边作如图所示的平行四边形ABCE,如图,若D是边AC中点,且BD=
| 7 |
| 2 |
解答:
 解:(Ⅰ) AB=5 , cos∠ABC=
解:(Ⅰ) AB=5 , cos∠ABC=
,BC=2,
由余弦定理:AC2=BA2+BC2-2BA•BC•cos∠ABC=52+22-2×5×2×
=25,∴AC=5. …(3分)
又∠ABC∈(0,π),所以sin∠ABC=
=
,
由正弦定理:
=
,
得sin∠ACB=
=
.…(6分)
(Ⅱ) 以BA,BC为邻边作如图所示的平行四边形ABCE,如图,
则cos∠BCE=-cos∠ABC=-
,BE=2BD=7,CE=AB=5,
在△BCE中,由余弦定理:BE2=CB2+CE2-2CB•CE•cos∠BCE.
即49=CB2+25-2×5×CB×(-
),
解得:CB=4. …(10分)
在△ABC中,AC2=BA2+BC2-2BA•BC•cos∠ABC=52+42-2×5×4×
=33,
即AC=
.…(12分)
 解:(Ⅰ) AB=5 , cos∠ABC=
解:(Ⅰ) AB=5 , cos∠ABC=| 1 |
| 5 |
由余弦定理:AC2=BA2+BC2-2BA•BC•cos∠ABC=52+22-2×5×2×
| 1 |
| 5 |
又∠ABC∈(0,π),所以sin∠ABC=
| 1-cos2∠ABC |
2
| ||
| 5 |
由正弦定理:
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
得sin∠ACB=
| AB×sin∠ABC |
| AC |
2
| ||
| 5 |
(Ⅱ) 以BA,BC为邻边作如图所示的平行四边形ABCE,如图,
则cos∠BCE=-cos∠ABC=-
| 1 |
| 5 |
在△BCE中,由余弦定理:BE2=CB2+CE2-2CB•CE•cos∠BCE.
即49=CB2+25-2×5×CB×(-
| 1 |
| 5 |
解得:CB=4. …(10分)
在△ABC中,AC2=BA2+BC2-2BA•BC•cos∠ABC=52+42-2×5×4×
| 1 |
| 5 |
即AC=
| 33 |
点评:本题考查余弦定理以及正弦定理的应用,三角形的解法,考查计算能力.

练习册系列答案
相关题目
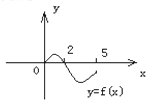 若一个函数y=f(x)的图象关于y轴对称,则称这个函数为偶函数,设偶函数y=f(x)的定义域为[-5,5],若当x∈[0,5]时,函数y=f(x)的图象如下图,则f(x)<0解集是( )
若一个函数y=f(x)的图象关于y轴对称,则称这个函数为偶函数,设偶函数y=f(x)的定义域为[-5,5],若当x∈[0,5]时,函数y=f(x)的图象如下图,则f(x)<0解集是( )| A、(-2,0)∪(2,5] |
| B、(-5,-2)∪(2,5) |
| C、[-2,0]∪(2,5] |
| D、[-5,-2)∪(2,5] |
设A={y|y=-1+x-2x2},若m∈A,则必有( )
| A、m∈{正有理数} |
| B、m∈{负有理数} |
| C、m∈{正实数} |
| D、m∈{负实数} |
设各项均不为0的数列{an}满足an+1=
an(n≥1),Sn是其前n项和,若a2a4=2a5,则S4=( )
| 2 |
A、4
| ||
B、8
| ||
C、3+3
| ||
D、6+6
|
已知集合A={x∈Z|x2-1≤0},B={x|x2-x-2=0},则A∩B=( )
| A、∅ | B、{-1} |
| C、{0} | D、{2} |
如图,正六边形ABCDEF的边长为1,则
•
=( )

| AD |
| DB |

| A、-3 | ||
B、-
| ||
| C、3 | ||
D、
|
 如图,已知椭圆
如图,已知椭圆